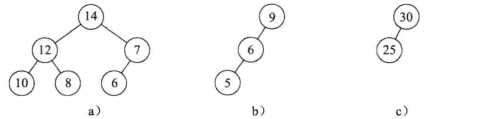
1.大根堆

1.1 定义

　　大根树：树中的每一个节点的值都大于或等于其子节点的值

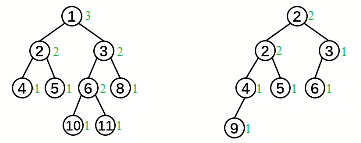
　　大根堆：既是大根树又是完全二叉树（增加了完全二叉树的限制条件）所以下图中只有(a)和(c)是大根堆

1.2 大根堆的插入（数组实现）

　　假设在下面大根堆中插入一个元素9，插入步骤如下，时间复杂度为O(height)=O(logn)

尝试插入在6号位置，如果新的元素小于3号位置，则插入；否则把3号位置的元素向下移动到6号位置
尝试插入在3号位置，如果新的元素小于1号元素，则插入；否则把1号位置的元素向下移动到3号位置，循环终止

// 为theElement寻找插入位置, currentNode从新叶子节点开始向上移动
int currentNode = ++heapSize;
while (currentNode != 1 && heap[currentNode / 2] < theElement)
{
    heap[currentNode] = heap[currentNode / 2]; // 元素向下移动
    currentNode /= 2;                          // currentNode移动到他的双亲
}

heap[currentNode] = theElement;

1.3 大根堆的出队

　　出队元素是最大的元素，也就是根节点，我们首先将1号元素删除，然后拿到最后一个元素，从上向下做插入的操作，时间复杂度为O(height)=O(logn)

// 从根节点开始, 为最后一个元素查找插入位置
int currentNode = 1;    // 当前双亲节点
int child = 2;          // 当前孩子节点
while (child <= heapSize)
{
    // heap[child] 应该是 currentNode 更大的孩子
    if (child < heapSize && heap[child] < heap[child + 1])
        child++;

    // 对比 lastElement 是否可以插入到 currentNode
    if (lastElement >= heap[child])
        break;   // 可以插入则直接结束

    // 不可以插入则继续循环
    heap[currentNode] = heap[child]; // 子节点向上移动
    currentNode = child;             // 当前指向节点移动到子节点
    child *= 2;
}
heap[currentNode] = lastElement;

1.4 大根堆的初始化

　　自下而上：从最后一个元素开始对比，到第一个元素结束，具体步骤如下

①找到孩子节点 2 和 7 中更大的元素，接下来与其双亲节点对比，7 更大所以交换 5 和 7 的位置
①找到孩子节点 7 和 6 中更大的元素，接下来与其双亲节点对比，7 更大所以交换 1 和 7 的位置；②找到孩子节点 2 和 5 中更大的元素，接下来与其双亲节点对比，5 更大所以交换 1 和 5 的位置

　　这里的循环包括两个步骤，第一个步骤是从下到上交换一次，第二个步骤是从上到下再检查一遍

// 堆化
for (int root = heapSize / 2; root >= 1; root--)
{
    T rootElement = heap[root];

    // 给元素 rootElement 寻找位置
    int child = 2 * root; // 孩子 child 的双亲是 rootElement 的位置
    // 确定 rootElement 的位置
    while (child <= heapSize)
    {
        // heap[child] 找到孩子里更大的那一个
        if (child < heapSize && heap[child] < heap[child + 1])
            child++;

        // 是否可以把 rootElement 插入到该位置
        if (rootElement >= heap[child])
            break;  // 可以

        // 不可以
        heap[child / 2] = heap[child]; // 孩子向上移动
        child *= 2;                    // 下移一层查看
    }
    heap[child / 2] = rootElement;
}

1.5 完整代码

1.5.1 优先级队列抽象父类

#pragma once
using namespace std;
template<class T>
class maxPriorityQueue
{
public:
    virtual ~maxPriorityQueue() {}
    // 队列是否为空
    virtual bool empty() const = 0;
    // 队列大小
    virtual int size() const = 0;
    // 返回优先级最高的元素
    virtual const T& top() = 0;
    // 弹出优先级最高的元素
    virtual void pop() = 0;
    // 插入元素
    virtual void push(const T& theElement) = 0;
};

1.5.2 大根堆的数组实现

#pragma once
#include "maxPriorityQueue.h"
#include <iostream>
#include <algorithm>

using namespace std;

template<class T>
class maxHeap : public maxPriorityQueue<T>
{
private:
    int heapSize;       // 队列中的元素数量
    int arrayLength;    // 队列的容量
    T* heap;            // 元素数组 

public:
    maxHeap(int initialCapacity = 10);
    ~maxHeap() { delete[] heap; }
    bool empty() const { return heapSize == 0; }
    int size() const { return heapSize; }
    const T& top()
    {// 返回优先级最大的元素
        if (heapSize == 0)
        {
            cout << "队列为空" << endl;
            return NULL;
        }
        return heap[1];
    }
    void pop();
    void push(const T&);
    void initialize(T*, int);
    void deactivateArray()
    {
        heap = NULL; arrayLength = heapSize = 0;
    }
    void output() const;
};


template<class T>
void changeLength(T*& a, int oldLength, int newLength)
{// 改变数组长度
    if (newLength < 1)return;
    T* temp = new T[newLength];              // 新的数组
    int number = min(oldLength, newLength);  // 需要复制的元素个数
    copy(a, a + number, temp);
    delete[] a;                              // 清理内存
    a = temp;
}

template<class T>
maxHeap<T>::maxHeap(int initialCapacity)
{// 构造函数
    if (initialCapacity < 1)
    {
        cout << "构造大根堆的数量必须大于1" << endl;
        return;
    }
    arrayLength = initialCapacity + 1;
    heap = new T[arrayLength];
    heapSize = 0;
}

template<class T>
void maxHeap<T>::push(const T& theElement)
{// 将元素插入到大根堆

   // 检查数组容量
    if (heapSize == arrayLength - 1)
    {
        changeLength(heap, arrayLength, 2 * arrayLength);
        arrayLength *= 2;
    }

    // 为theElement寻找插入位置, currentNode从新叶子节点开始向上移动
    int currentNode = ++heapSize;
    while (currentNode != 1 && heap[currentNode / 2] < theElement)
    {
        heap[currentNode] = heap[currentNode / 2]; // 元素向下移动
        currentNode /= 2;                          // currentNode移动到他的双亲
    }

    heap[currentNode] = theElement;
}

template<class T>
void maxHeap<T>::pop()
{// 从大根堆删除最大的元素

    if (heapSize == 0)   // 大根堆是否为空
        return;

    // 删除最大的元素
    heap[1].~T();

    // 拿到最后一个元素, 并将大根堆元素数量减1
    T lastElement = heap[heapSize--];

    // 从根节点开始, 为最后一个元素查找插入位置
    int currentNode = 1;    // 当前双亲节点
    int child = 2;          // 当前孩子节点
    while (child <= heapSize)
    {
        // heap[child] 应该是 currentNode 更大的孩子
        if (child < heapSize && heap[child] < heap[child + 1])
            child++;

        // 对比 lastElement 是否可以插入到 currentNode
        if (lastElement >= heap[child])
            break;   // 可以插入则直接结束

        // 不可以插入则继续循环
        heap[currentNode] = heap[child]; // 子节点向上移动
        currentNode = child;             // 当前指向节点移动到子节点
        child *= 2;
    }
    heap[currentNode] = lastElement;
}

template<class T>
void maxHeap<T>::initialize(T* theHeap, int theSize)
{// 在数组 theHeap[1:theSize] 中初始化大根堆
    delete[] heap;
    heap = theHeap;
    heapSize = theSize;

    // 堆化
    for (int root = heapSize / 2; root >= 1; root--)
    {
        T rootElement = heap[root];

        // 给元素 rootElement 寻找位置
        int child = 2 * root; // 孩子 child 的双亲是 rootElement 的位置
        // 确定 rootElement 的位置
        while (child <= heapSize)
        {
            // heap[child] 找到孩子里更大的那一个
            if (child < heapSize && heap[child] < heap[child + 1])
                child++;

            // 是否可以把 rootElement 插入到该位置
            if (rootElement >= heap[child])
                break;  // 可以

            // 不可以
            heap[child / 2] = heap[child]; // 孩子向上移动
            child *= 2;                    // 下移一层查看
        }
        heap[child / 2] = rootElement;
    }
}

template<class T>
void maxHeap<T>::output() const
{
    for (int i = 1; i < heapSize; i++)
    {
        cout << this->heap[i] << " ";
    }
    cout << endl;
}

2.左高树

2.1 高度优先左高树和重量优先左高树

　　左高树合并操作的时间复杂度更低，适合需要合并操作较多的数据

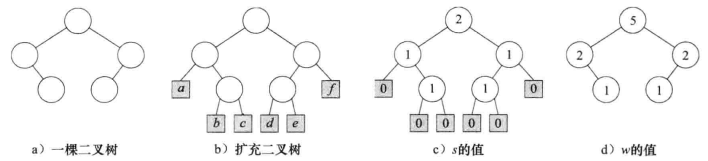
　　定义一类特殊的节点为外部节点来代替空子树，其余节点为内部节点。增加了外部节点的二叉树称为扩充二叉树。

　　定义距离s：s 是该节点到外部节点的最短路径。

　　定义重量w：w 是该节点重量的和，节点本身重量为1，节点的重量为自身重量与孩子重量的和。

　　高度优先左高树（height-biased leftist tree，HBLT）：这个二叉树任何一个内部节点左孩子的 s 值都大于等于右孩子的 s 值。其中上图(a)就不是一棵左高树，因为它左侧子树的左孩子值为0，而右孩子值为1，下图是2个HBLT。

　　重量优先左高树（weight-biased leftist tree，WBLT）：这个二叉树任何一个内部节点左孩子的 w 值都大于或等于右孩子的 w 值。

2.2 HBLT的性质

堆的性质：任意节点值的大小 ≤ 其孩子节点的大小（小根堆，也可以是 ≥ ）
左偏性质：左孩子的距离 s ≥ 右孩子的距离 s
任意节点的距离 s 都等于其右孩子的距离 + 1
一棵有 n 个节点的二叉树，根的距离dis ≤ long(n+1) - 1（距离最远就是满二叉树的情况，否则一定有更短路径出去）

2.3 HBLT的插入和删除

　　插入相当于将已有的树和一棵仅有一个元素的树进行合并操作

　　删除相当于将左右两棵HBLT进行合并操作

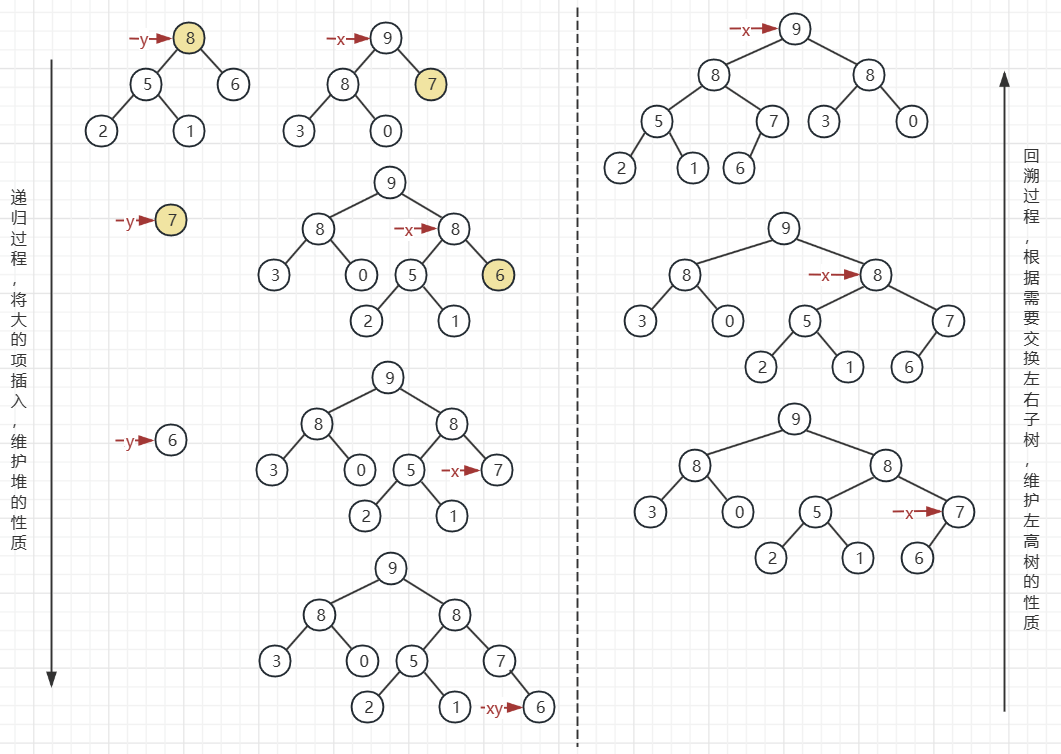
2.4 HBLT的合并（链式实现）

　　用一张图解释合并的过程，我们需要把两棵树合并到 x 上

对比 x 指向节点数值和 y 指向节点数值的大小
如果节点数值 x < y，则将 x 指向的地址和 y 指向的地址交换
将 x 指针移动到 x 的右孩子位置

　　这就是图左完整的递归过程，递归的过程实际上就是在比较两个左高树右侧孩子链的大小，并来回交换来保证堆的性质，所以整个递归应该是O(logm)+O(logn)的时间复杂度

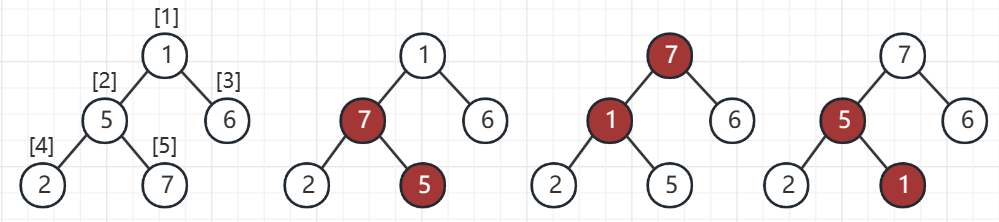
首先 x 移动到下一个位置指向元素 7，对比元素 7 和元素 8，元素 8 更大，所以指针指向的地址互换，元素 8 移动到右孩子的位置
然后 x 移动到下一个位置指向元素 6，对比元素 6 和元素 7，元素 7 更大，所以指针指向的地址呼唤，元素 7 移动到右孩子的位置
然后 x 移动到下一个位置指向 NULL，因为 x 指向 NULL，所以直接将 x 指向 y 所指向的地址，递归结束

　　最后一步是回溯，已经完成元素的插入后，需要维护左高树的性质，回溯的过程就是根据距离不断交换孩子节点的位置，保证左孩子的距离 ≥ 右孩子的距离

template<class T>
void maxHblt<T>::merged(binaryTreeNode<pair<int, T> >*& x, binaryTreeNode<pair<int, T> >*& y)
{// 合并两棵左高树, x是自己的根节点地址, y是传入的根节点地址
    if (y == NULL)   // 如果传入的树为空, 不需要操作
        return;
    if (x == NULL)   // 如果x节点为空, 则直接让该节点的值等于传入节点的值
    {
        x = y; return;
    }

    // 维护堆的性质, 保证 x 是更大的那一个
    if (x->element.second < y->element.second)
        swap(x, y);

    // 接下来进行递归, x 向其右孩子移动一位
    merged(x->rightChild, y);

    // 最后是回溯的过程, 需要维护左高树的性质, 保证左孩子的路径长度大于右孩子
    if (x->leftChild == NULL)
    {// 左树为空直接交换即可
        x->leftChild = x->rightChild;
        x->rightChild = NULL;
        x->element.first = 1;
    }
    else
    {// 左树不为空则对比他们的路径长度
        if (x->leftChild->element.first < x->rightChild->element.first)
            swap(x->leftChild, x->rightChild);
        // 最后更新路径长度
        x->element.first = x->rightChild->element.first + 1;
    }
}

2.5 HBLT的初始化

template<class T>
void maxHblt<T>::initialize(T* theElements, int theSize)
{// 根据给定的数组初始化左高树
    arrayQueue<binaryTreeNode<pair<int, T> >*> q(theSize);

    // 初始化树的队列
    for (int i = 1; i <= theSize; i++)
        // 建立一个只有一个节点的树插入队列
        q.push(new binaryTreeNode<pair<int, T> >
            (pair<int, T>(1, theElements[i])));

    // 从队列中重复取出树进行合并操作
    for (int i = 1; i <= theSize - 1; i++)
    {// 从队列中取出2个树
        binaryTreeNode<pair<int, T> >* b = q.front();
        q.pop();
        binaryTreeNode<pair<int, T> >* c = q.front();
        q.pop();
        merged(b, c);
        // 把合并后的树插入队列
        q.push(b);
    }

    if (theSize > 0)
        this->root = q.front();
    this->treeSize = theSize;
}