1.栈

1.1栈的抽象父类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#pragma once
template<class T>
class Stack
{
public:
    // 析构函数
    virtual ~Stack() {}
    // 栈是否为空
    virtual bool empty() const = 0;
    // 栈的大小
    virtual int size() const = 0;
    // 栈顶元素
    virtual T& top() = 0;
    // 出栈
    virtual void pop() = 0;
    // 入栈
    virtual void push(const T& theElement) = 0;
};

1.2栈的数组实现

【数据结构】1.线性表的数组描述和链式描述 - imXuan - 博客园 (cnblogs.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#pragma once
#include"stack.h"
#include"arrayList.hpp"
#include<iostream>
using namespace std;
template<class T>
class DerivedArrayStack :private ArrayList<T>, public Stack<T>
{
public:
    DerivedArrayStack(int initialCapacity = 10) :ArrayList<T>(initialCapacity) {}
    // 栈是否为空
    bool empty() const { return ArrayList<T>::empty(); }
    // 栈的大小
    int size() const { return ArrayList<T>::size(); }
    // 栈顶元素
    T& top() 
    {
        if (ArrayList<T>::empty())
            cout << "栈为空" << endl;
        else 
            return ArrayList<T>::get(ArrayList<T>::size() - 1);
    }
    // 出栈
    void pop()
    {
        if (ArrayList<T>::empty())
            cout << "栈为空" << endl;
        else
        {
            cout << "出栈元素为：" << ArrayList<T>::get(ArrayList<T>::size() - 1) << endl;
            ArrayList<T>::erase(ArrayList<T>::size() - 1);
        }            
    }
    // 入栈
    void push(const T& theElement)
    {
        ArrayList<T>::insert(ArrayList<T>::size(), theElement);
    }
};

1.3栈的链式实现

【数据结构】1.线性表的数组描述和链式描述 - imXuan - 博客园 (cnblogs.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#pragma once
#include"chain.hpp"
#include"stack.h"
#include<iostream>
using namespace std;
template<class T>
class DerivedLinkedStack :private Chain<T>, public Stack<T>
{
public:
    DerivedLinkedStack(int initialCapacity = 10) :Chain<T>(initialCapacity) {}
    // 栈是否为空
    bool empty() const { return Chain<T>::empty(); }
    // 栈的大小
    int size() const { return Chain<T>::size(); }
    // 栈顶元素
    T& top()
    {
        if (Chain<T>::empty())
            cout << "栈为空" << endl;
        else
            return Chain<T>::get(Chain<T>::listSize - 1);
    }
    // 出栈
    void pop() 
    {
        if (Chain<T>::empty())
            cout << "栈为空" << endl;
        else
        { 
            cout << "出栈元素为：" << Chain<T>::get(Chain<T>::listSize - 1) << endl;
            Chain<T>::erase(Chain<T>::listSize - 1);
        }
    }
    // 入栈
    void push(const T& theElement)
    {
        Chain<T>::insert(Chain<T>::size(), theElement);
    }
};

2.队列

2.1队列的抽象父类

1
2
3
4
5
6
7
8
9
10
11
12
13
#pragma once
template<class T>
class queue
{
public:
    virtual ~queue() {}
    virtual bool empty() const = 0;
    virtual int size() const = 0;
    virtual T& front() = 0;
    virtual T& back() = 0;
    virtual void pop() = 0;
    virtual void push(const T& theElement) = 0;
};

2.2队列的数组实现

队列由一个数组来描述，队首指针是队首的前一个元素，队尾指针是队尾所在元素，当队首和队尾指针重叠时表示队列为空；当 (队尾指针+1)%数组长度 等于队首指针时队列为满

img

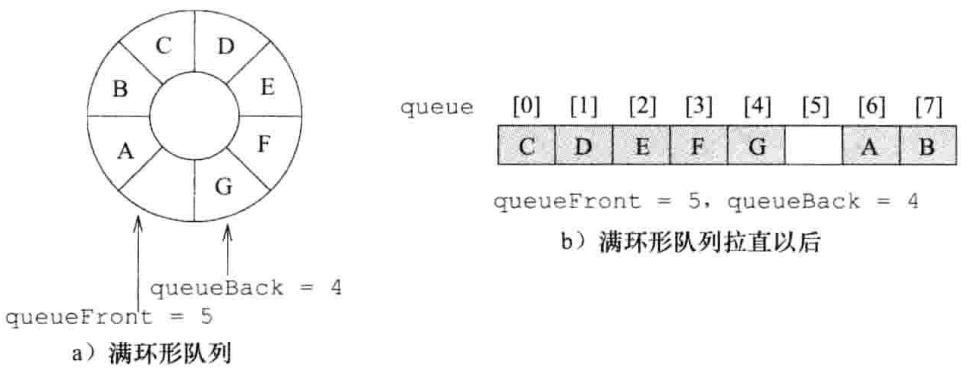
假设push数据时队列已满，需要为存储队列的数组进行扩充，我们将AB首先移动到起始位置，然后将C~G移动到AB之后，具体代码参见 push()

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#pragma once
#include"queue.h"
#include"arrayList.hpp"
#include<iostream>
using namespace std;
template<class T>
class arrayQueue :public queue<T>
{
private:
    int theFront;       // 第一个元素的前一个
    int theBack;        // 最后一个元素
    int arrayLength;    // 队列长度
    T* queue;           // 队列本体
public:
    arrayQueue(int initialCapacity = 10);
    ~arrayQueue() { delete[] queue; }
    bool empty() const { return theFront == theBack; }
    int size() const
    {
        return (theBack - theFront + arrayLength) % arrayLength;
    }
    T& front()
    {
        if (theFront == theBack)
        {
            cout << "队列为空" << endl;
        }
        return queue[(theFront + 1) % arrayLength];
    }
    T& back()
    {
        if (theFront == theBack)
        {
            cout << "队列为空" << endl;
        }
        return queue[theBack];
    }
    void pop()
    {
        if (theFront == theBack)
        {
            cout << "队列为空" << endl;
            return;
        }
        cout << queue[(theFront + 1) % arrayLength];
        theFront = (theFront + 1) % arrayLength;
        queue[theFront].~T();
    }
    void push(const T& theElement);
};


template<class T>
arrayQueue<T>::arrayQueue(int initialCapacity)
{
    if (initialCapacity < 1)
    {
        cout << "initialCapacity 必须为正整数" << endl;
        return;
    }
    arrayLength = initialCapacity;
    queue = new T[arrayLength];
    theFront = 0;
    theBack = 0;
}

template<class T>
void arrayQueue<T>::push(const T& theElement)
{
    if ((theBack + 1) % arrayLength == theFront)
    {
        T* newQueue = new T[2 * arrayLength];

        int start = (theFront + 1) % arrayLength;
        if (start < 2)
            copy(queue + start, queue + start + arrayLength - 1, newQueue);
        else
        {
            copy(queue + start, queue + arrayLength, newQueue);
            copy(queue, queue + theBack + 1, newQueue + arrayLength - start);
        }

        theFront = 2 * arrayLength - 1;
        theBack = arrayLength - 2;
        arrayLength *= 2;
        queue = newQueue;
    }

    theBack = (theBack + 1) % arrayLength;
    queue[theBack] = theElement;
}

2.3队列的链式实现

【数据结构】1.线性表的数组描述和链式描述 - imXuan - 博客园 (cnblogs.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#pragma once
#include "queue.h"
#include "chainNode.hpp"
#include <iostream>
using namespace std;

template<class T>
class linkedQueue : public queue<T>
{
private:
    chainNode<T>* queueFront;  // 头指针
    chainNode<T>* queueBack;   // 尾指针
    int queueSize;             // 队列大小

public:
    linkedQueue(int initialCapacity = 10)
    {
        queueFront = NULL; queueSize = 0;
    }
    ~linkedQueue();
    bool empty() const {return queueSize == 0；}
    int size() const { return queueSize；}
    T& front()
    {
        if (queueSize == 0)
            cout << "队列为空" << endl;
        return queueFront->element;
    }
    T& back()
    {
        if (queueSize == 0)
            cout << "队列为空" << endl;
        return queueBack->element;
    }
    void pop();
    void push(const T&);
};

template<class T>
linkedQueue<T>::~linkedQueue()
{
    while (queueFront != NULL)
    {
        chainNode<T>* nextNode = queueFront->next;
        delete queueFront;
        queueFront = nextNode;
    }
}

template<class T>
void linkedQueue<T>::pop()
{
    if (queueFront == NULL)
    {
        cout << "队列为空" << endl;
        return;
    }
    chainNode<T>* nextNode = queueFront->next;
    delete queueFront;
    queueFront = nextNode;
    queueSize--;
}

template<class T>
void linkedQueue<T>::push(const T& theElement)
{
    chainNode<T>* newNode = new chainNode<T>(theElement, NULL);

    if (queueSize == 0)
        queueFront = newNode;
    else
        queueBack->next = newNode;
    queueBack = newNode;

    queueSize++;
}