2.1 信息存储
机器级的程序将存储器视为一个字节数组,称为虚拟存储器(virtual memory)。存储器的每个字节都由一个唯一数字标识,称为该字节的地址(address),所有地址的集合称为虚拟地址空间(virtual address space)。
2.1.1 字
每台计算机都有一个字长(word size),指明整数和指针数据的标称大小(norminal size)。虚拟地址就是这么编码的,对于32位字长的计算机,限制了他的虚拟地址空间位232-1位4GB,对于64位字长的计算机,内存最大支持128G。
2.1.2 寻址和字节顺序
一个对象存储有大端法和小端法,最低有效位在最前面的方式被称为小端法,另一种称为大端法。许多芯片在加电启动时确定字节顺序规则。假设有一个0x1234567在地址范围0x100~0x103存储,顺序如下
| 大端法 | 0x100 | 0x101 | 0x102 | 0x103 | |
|---|---|---|---|---|---|
| … | 01 | 23 | 45 | 67 | … |
| 小端法 | 0x100 | 0x101 | 0x102 | 0x103 | |
|---|---|---|---|---|---|
| … | 67 | 45 | 23 | 01 | … |
2.1.3 布尔代数和环
“~”:逻辑运算NOT
“&”:逻辑运算AND
“ | “:逻辑运算OR
“ ^ “:异或运算EXCLUSIVE-OR,PQ为真但不全为真时成立
| ~ | & | 0 | 1 | | | 0 | 1 | ^ | 0 | 1 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |||
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
2.1.4 位级运算
| C的表达式 | 二进制表达式 | 二进制结果 | C的结果 |
|---|---|---|---|
| ~0x41 | ~[01000001] | [10111110] | 0xBE |
| ~0x00 | ~[00000000] | [11111111] | 0xFF |
| 0x69&0x55 | [01101001]&[01010101] | [0100001] | 0x41 |
| 0x69 | 0x55 | [01101001] | [01010101] | [01111101] | 0x7D |
| x << k | 将x向左移动k位,丢掉k个最高位,右端补k个0 |
2.2 整数表示
一个整数数据类型有 w 位,可以写成[xw-1, xw-2, …, x0],可以得到无符号数的二进制表示形式(式1)
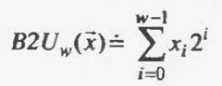
在计算机中希望使用二进制补码形式表现有符号数(负数),其中最高位解释为负权或符号位,正数的原码、反码、补码都相等,负数的反码是除符号位外取反,补码等于反码加1(式2)
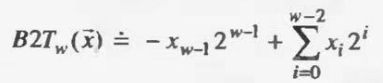
| 数字 | 原码 | 反码 | 补码 | 直接计算 |
|---|---|---|---|---|
| -128 | 无 | 无 | 1000 0000 | -27= - 128 |
| -127 | 1111 1111 | 1000 0000 | 1000 0001 | -27+1=-127 |
| -10 | 1000 1010 | 1111 0101 | 1111 0110 | -27+26+25+24+22+21=-10 |
| 10 | 0000 1010 | 0000 1010 | 0000 1010 | 23+21=10 |
| 127 | 0111 1111 | 0111 1111 | 0111 1111 | 26+25+24+23+22+21+20=127 |
从这里理解有符号数和无符号数的映射,有符号数的正数部分对应了无符号数相同大小的正数部分,而有符号数负数的部分对应了更大的无符号数部分,反过来无符号数较大的部分会对应有符号数的负数

对于数字的截断,如果将一个32位整数截断到16位,会截断32位前面的16位,保留后面的16位
2.3 整数运算
2.3.1 无符号加法
无符号运算可以被视为一种模的运算。例如考虑一个四位数表示,x=9和y=12,[1001]和[1100]。它们的和是21,五位表示为[10101],但如果截断最高位会得到[0101],也就是5,这和 21 mod 16 = 5一致
2.3.2 二进制补码加法
二进制补码运算中存在移除情况,根据式2可以很好理解,0111 1111是正数最大值,而1000 0000是负数最小值,所以正数向上溢出后会是最小的负数,而负数向下溢出后是最大的正数
2.3.3 二进制补码的非
以8位举例说明,范围-128≤x<128中的每个数字都有一个逆元,对于x≠-128的时候,他的逆元就是-x(因为-128的逆元128没办法用这8位来表示)。
求逆元的方式是按位取反再加1,即-x = ~x+1。
2.3.4 乘法/除法和移位操作
以7位举例说明无符号数,对于范围0≤x,y≤127内的整数,x和y的乘积在取值范围0到127127之间,但是最后只会保留后7位,所以实际上形成了一个环,计算实际上保留的是(xy) mod 127
计算机中乘法指令一般需要12或更多的时钟周期,而加法减法只需要1个时钟周期,因此编译器一般会对常数乘法修改为移位运算
例如2x就相当于x<<1,将x左移一位,而3x就相当于(x<<1) + x,将x左移一位并在末尾+1,同理除法会做右移
| 数 | 计算 | 二进制表示 | 操作 | 新的二进制表示 | 最终得到 |
|---|---|---|---|---|---|
| 无符号 | 5 * 3 | 0101(补) | 左移 1 位并加他本身 | 1111(补) -> 1111(原) | 15 |
| 有符号 | 5 / 2 | 0101(补) | 右移 1 位(符号位不变,高位补0) | 0010(补)-> 0010(原) | 2 |
| 有符号 | -5 / 2 | 1011(补) | 右移 1 位(符号位不变,高位补1) | 1101(补)-> 1011(原) | -3 |
2.4 浮点数
2.4.1 二进制小数
12.3410表示数字1×101+2×100+3×10-1+4×10-2=12又(34/100)
10.1112表示数字21+0+2-1+2-2+2-3=2又(7/8)
注意二进制实际上只能准确表示可以写成x × 2y的数,比如准确表示21, 22, 2-1, 3*2-4, 对于1/5因为没有办法准确描述成前面的形式,所以没办法准确表示0.2
2.4.2 IEEE 浮点表示
IEEE 浮点标准用 V = (-1)s × 2E × M的形式来表示一个数,其中s表示正数或负数,M是一个二进制小数,范围在12-ε或01-ε之间,E表示对浮点数的加权
在C语言32位精度浮点数中,符号位1位,加权8位,小数域23位;64位浮点数的加权有11位,小数域有52位。
- 规格化值:对于指数位不全为0或全为1的情况,指数的值为 E = e - Bias(e为指数位的值,偏置Bias是2k-1),此时小数域定义位1,x,x,x,x,首位默认有一个1
- 非规格化值:对于指数全0的情况,指数值E = 1 - Bias,有效值M = f
- 特殊值:对于指数全1的情况,若小数域全0,表示无穷,s=0是正无穷,s=1是负无穷;如果小数域非全0表示NaN,比如√-1就是NaN
下面假设有一个8位浮点数,其中有k=4的指数位和n=3的小数位,Bias = 24-1 = 7,下表是8位浮点数的非负表示示例,完整读一遍就可以理解该表示了。可以发现定义非规格化的的偏置是1 - Bias,并且在规格化数的首位加1bit可以实现最大非规格化数到最小规格化数的平滑过渡,这7位可以表示的数实际上一共是非规格化数23个,规格化数23×(24-2)个,一共23×(24-1)个,本质上就是没有了指数位全1情况下的表示。而且这种在首位加1的方式实际上是因为全0表示的时候已经进了1位。
| 描述 | 位表示 | 指数值 | 偏置后指数值 | 小数域 | 有效小数值 | 实际值 | |
|---|---|---|---|---|---|---|---|
| 非规格****化 | 0 | 0 0000 000 | 0 | 1 - Bias = -6 | 0/8 | 0/8 | 0 |
| 最小的非规格化数 | 0 0000 001 | 0 | 1 - Bias = -6 | 1/8 | 1/8 | 1/8 * 2-6 = 1/512 | |
| 最大的非规格化数 | 0 0000 111 | 0 | 1 - Bias = -6 | 7/8 | 7/8 | 7/8 * 2-6 = 7/512 | |
| 规格化 | 最小的规格化数 | 0 0001 000 | 1 | e - Bias = -6 | 0/8 | 8/8 | 8/8 * 2-6 = 8/512 |
| 1 | 0 0111 000 | 7 | e - Bias = 0 | 0/8 | 8/8 | 8/8 * 20 = 8/8 | |
| 最大的规格化数 | 0 1110 111 | 14 | e - Bias = 7 | 7/8 | 15/8 | 15/8 * 214 = 240 | |
| 特殊值 | 无穷大 | 0 1111 000 | 符号位为0,指数位全1,小数位全0表示正无穷 | ||||
| NaN | 0 1111 010 | 指数位全1,小数位非全0表示NaN |
2.4.3 浮点运算
IEEE标准定义+∞-∞=NaN,任何数+NaN都是NaN,其他情况就是正常的计算,但要注意大数吃小数的情况
举例3.14+1e10-1e10得到的将会是0,因为顺序计算第一次的时候3.14已经被精度问题舍入了,而3.14+(1e10-1e10)会得到正确的值,在判断值的大小进入函数体内的方法中需要注意
参考文献
深入理解计算机系统(第三版)