1.Unity渲染管线综述

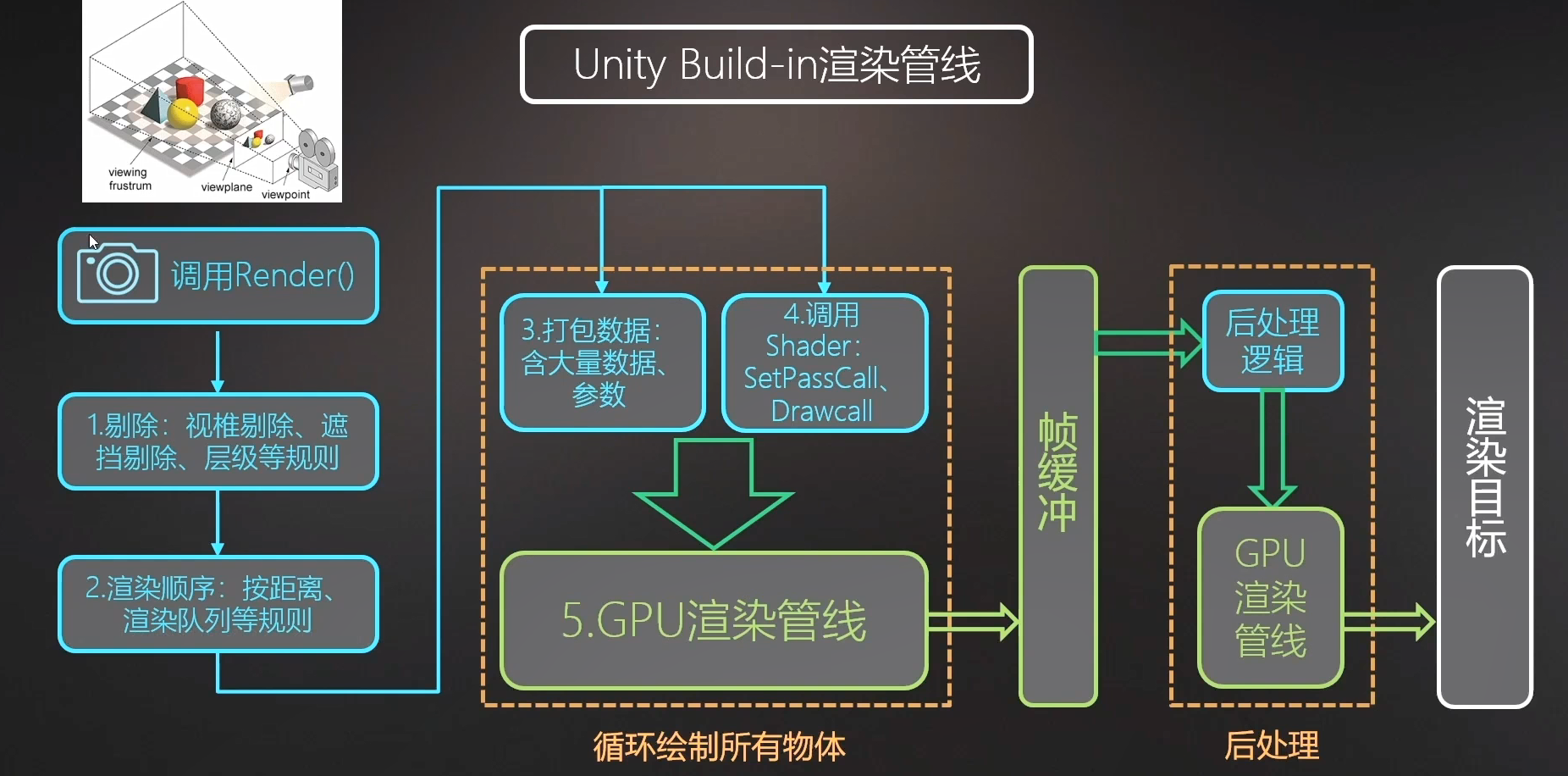
1.1CPU“应用程序阶段”

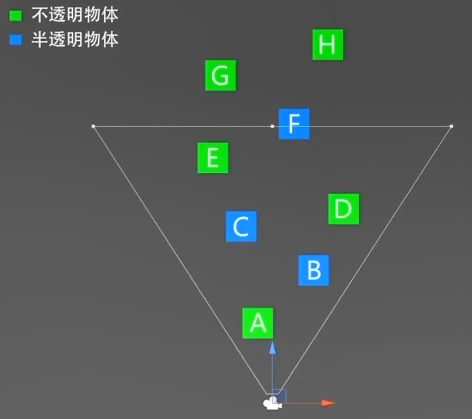
  • 剔除（Culling）：

视锥体剔除（Frustum Culling）

层级剔除（Layer Culling Mask），遮挡剔除（Occlusion Culling）等

  • 排序（Sort）：

渲染队列（RenderQueue）

不透明队列（RenderQueue<2500）按摄像机从前向后渲染

半透明队列（RenderQueue>2500）按摄像机从后向前渲染

（RenderQueue在shader里，前靠近摄像头，后原理摄像头）

  • 打包数据（Batch）

模型信息、变换矩阵、灯光、材质参数 ，加载到现存

  • 绘制调用（DrawCall、SetPass）

1.2GPU渲染管线

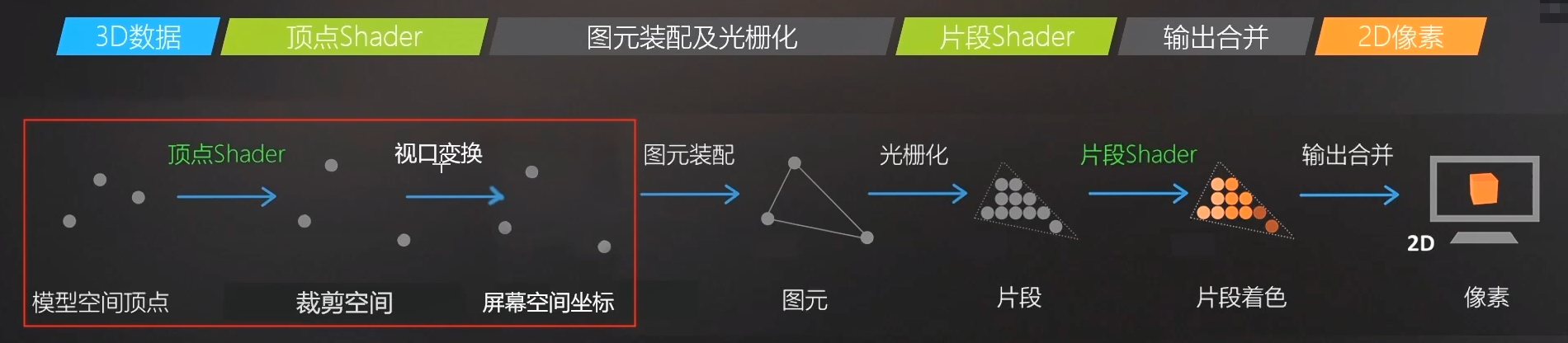
CPU输入顶点数据后，进入GPU工作流程

阶段 操作名称 作用
几 何 阶 段 顶点着色器（Vertex Shader） 完全可编程，顶点空间变换、顶点着色
曲面细分着色器（Tessellation Shader） 可选，细分图元
几何着色器（Geometry Shader） 可选，逐行执行图片着色操作，或产生更多图元
裁剪（Clipping） 将不在摄像机视野的三角面顶点裁剪
屏幕映射（Screen Mapping） 不可配置和编程，将图元坐标转换到屏幕坐标
光 栅 化 阶 段 三角形设置（Triangle Setup） 光栅化一个三角网格所需的信息，使顶点生成网格
三角形遍历（Triangle Traversal） 检测每个像素是否被三角形网格覆盖，如果覆盖则生成一个片元（fragment）
片元着色器（Fragment Shader） 重要技术之一是纹理采样
逐片元操作（Per-Fragment Operations） 模板测试→深度测试。通过后将颜色值和颜色缓冲区中的颜色混合

经过GPU流水线后，图象被输出到屏幕上

1.1.1 光栅化

1
2
3
4
for(int x = 0; x \< xmax ; x++)
for(int y = 0; y \< ymax ; y++)
inside(try, x+0.5, y+0.5) //是inside自己定义的函数，判断像素是否在连线内
//P0P2 × P0Q、P2P1 × P2Q、P1P0×P1Q 叉乘结果应该符号相同

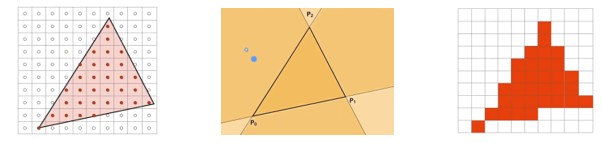
由于光栅化的过程会出现走样的情况，锯齿很明显，提出了模糊的方法来解决锯齿问题，先把信号的高频信号拿掉，再进行采样。

1.1.2 滤波

高通滤波，只显示高通信息，即对比度信息较高的信息；低通滤波与之相反，保留对比度较低的信息

可以理解为对该像素的信号做一个加权的平均值，取附近的信号和该像素的信号。比如右图3×3

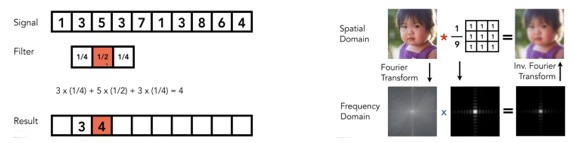
MSAA，把1个像素当成4个像素进行处理来抗锯齿。还有FXAA、TAA、DLSS方法抗锯齿

1.1.3 深度缓存

//注，图形学中摄像机z轴正方向为从屏幕指向屏幕外，这里为了方便理解，将z轴指向屏幕内，所以数字越大深度越深

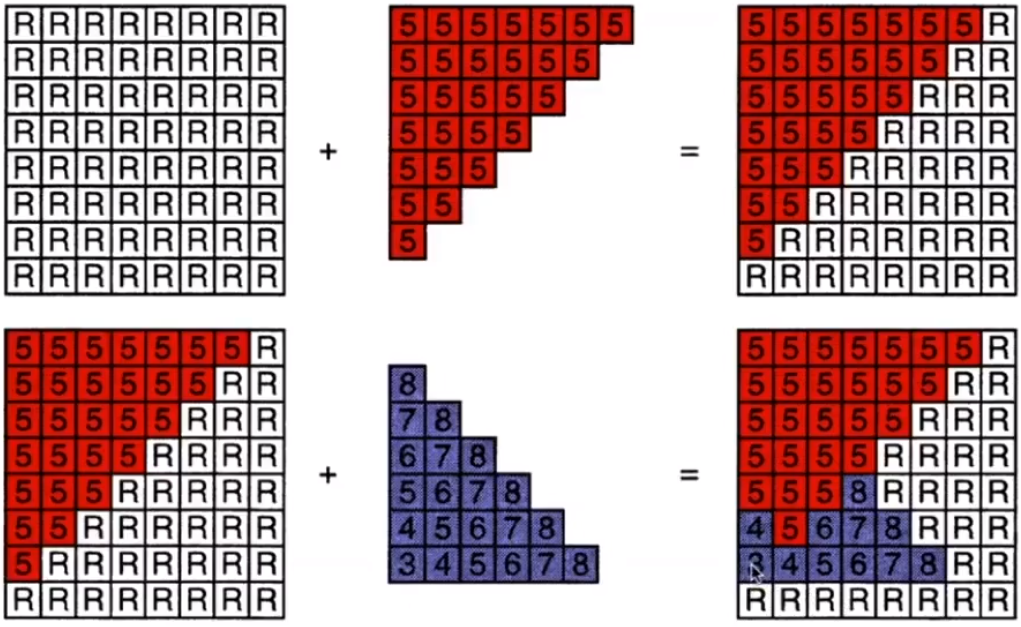
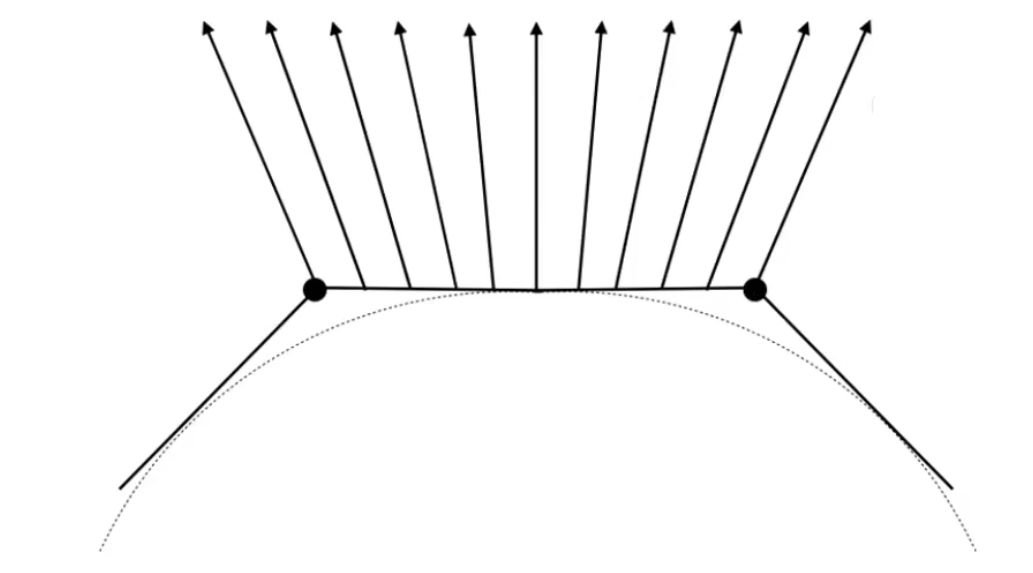
1.1.4 兰伯特定律和光线能量衰减

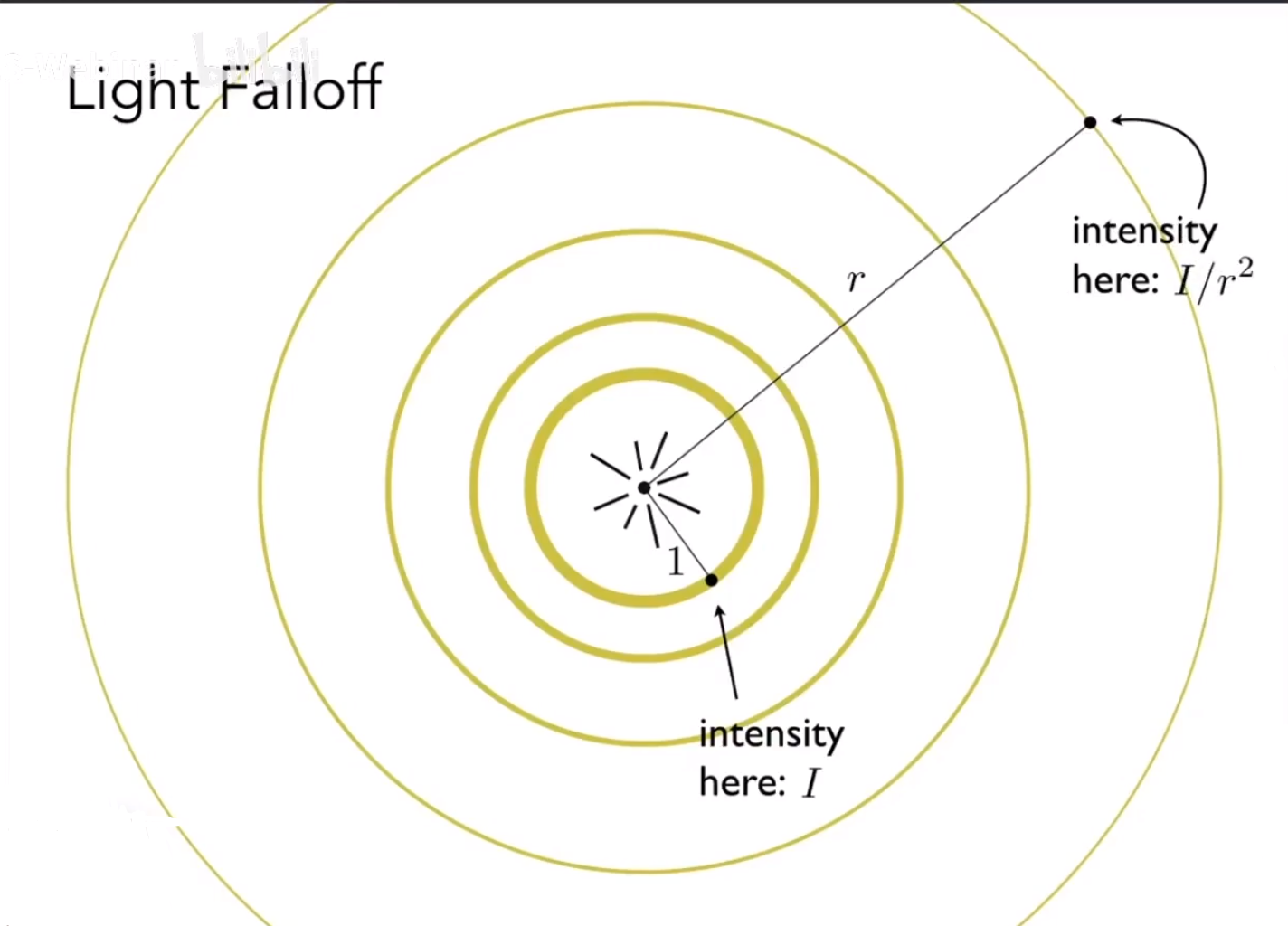
我们认为光的能量

在每一个球壳上是完全相等的

也就是说光的能量与半径的平方成反比

能量=I/r2

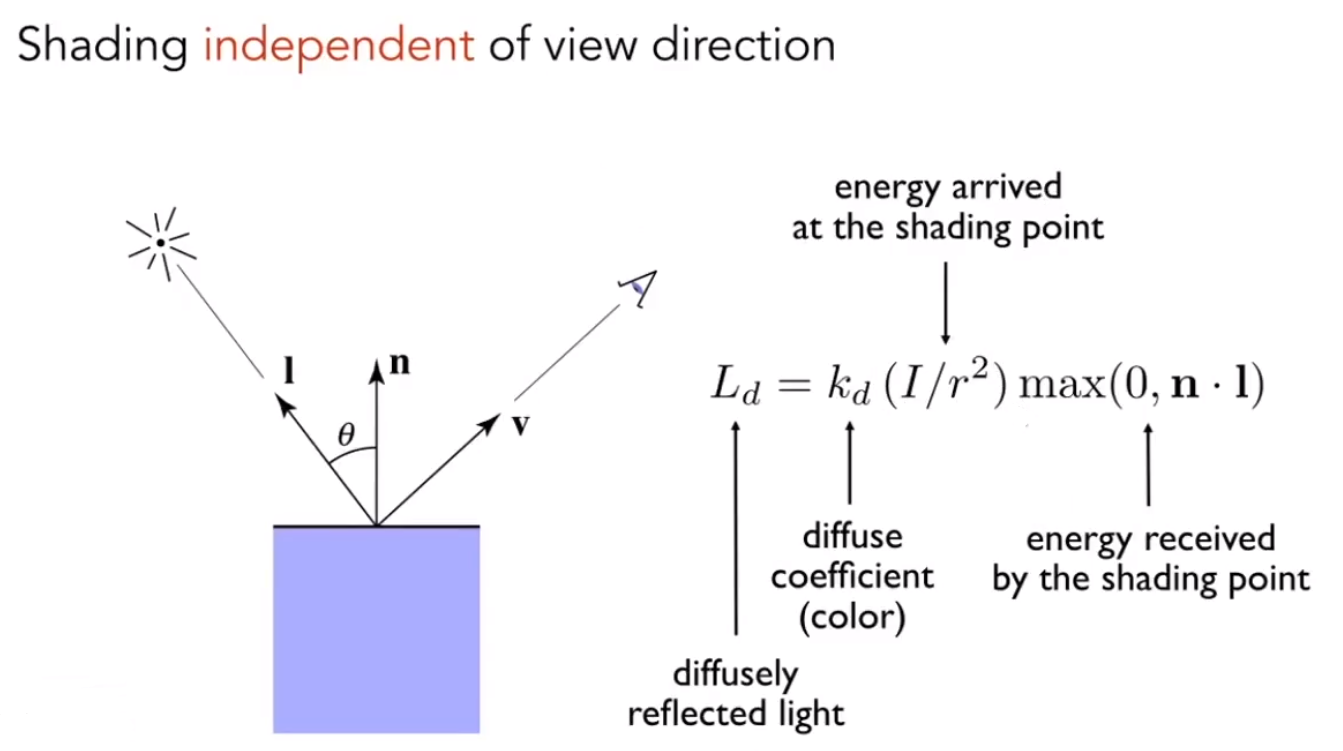
我们获得了光的能量计算方法

所以可以获得光能量影响下的兰伯特公式

Ld=kd(I/r2)max(0, n·l)

1.1.5 Blnn-Phong高光模型

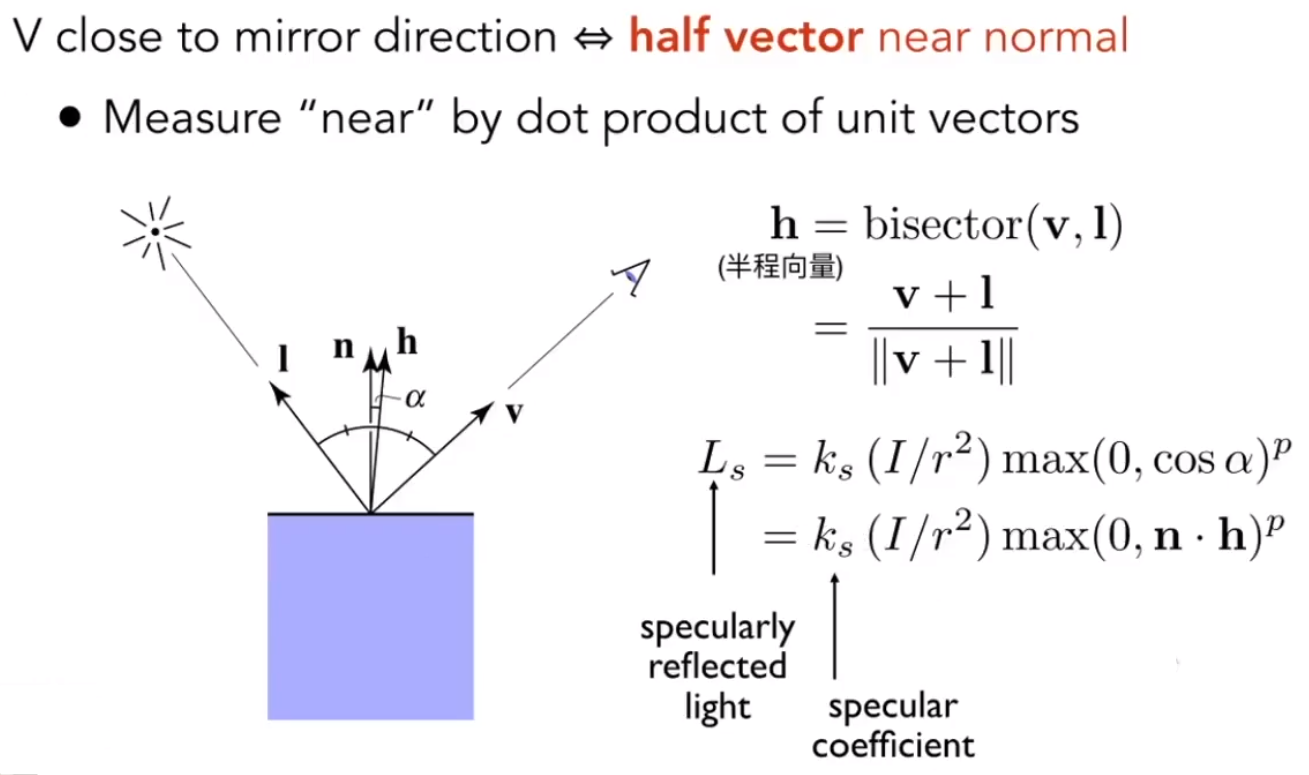
高光处p的指数主要用于缩小高光的范围，高光应该是人眼观测角度很小时才有的现象

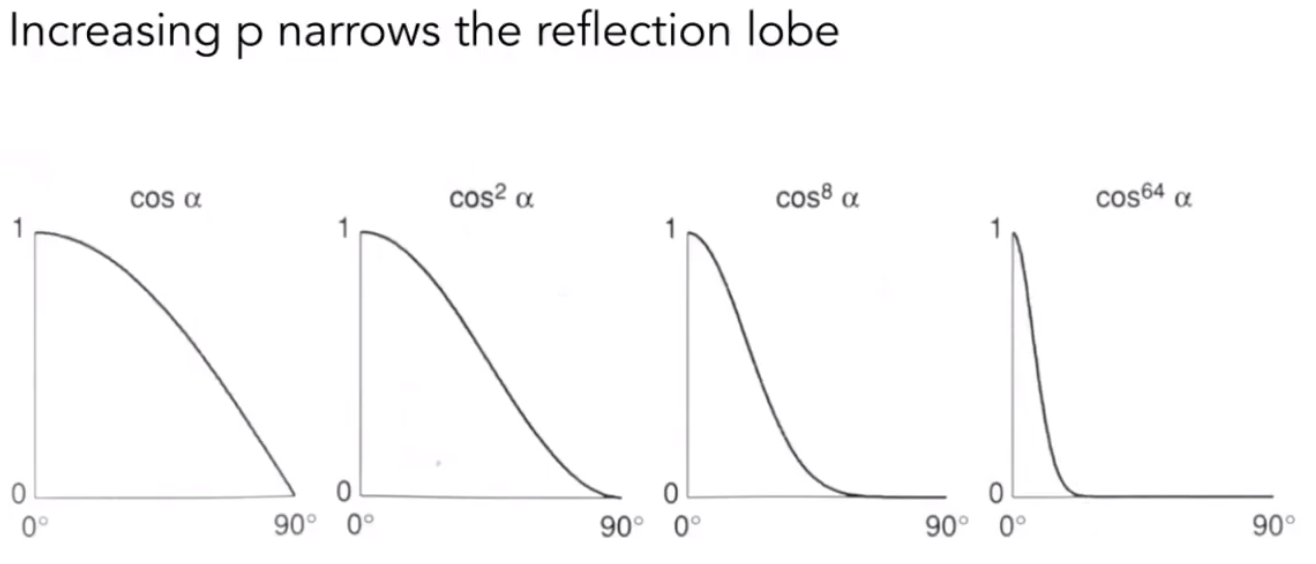
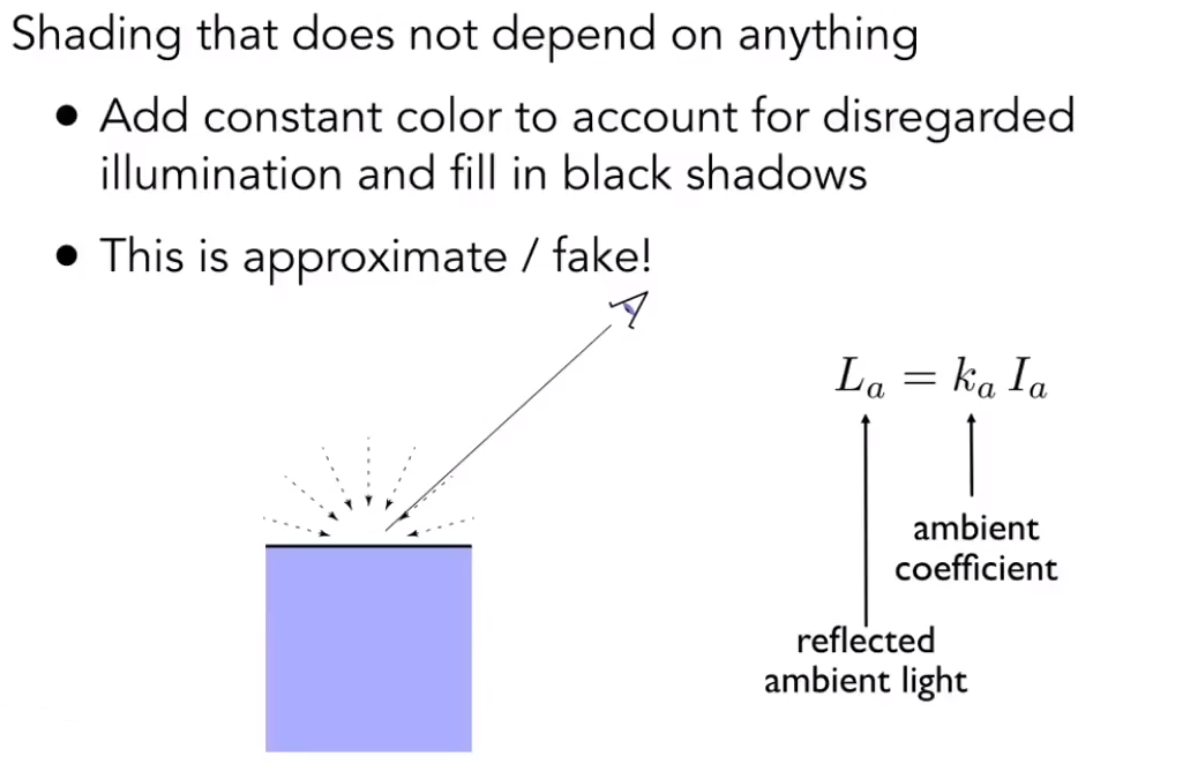
1.1.6 Ambient环境光

环境光可以理解为是一个均匀的光，整体完全提亮

1.1.7 Blnn-Phong Reflection Model

1.1.8 渲染的三种形式

三种渲染模式：每个面的法线、每个顶点的法线、每个像素的法线

每个顶点法线的计算就是通过每个面的法线，经过加权平均以后获得顶点的法线

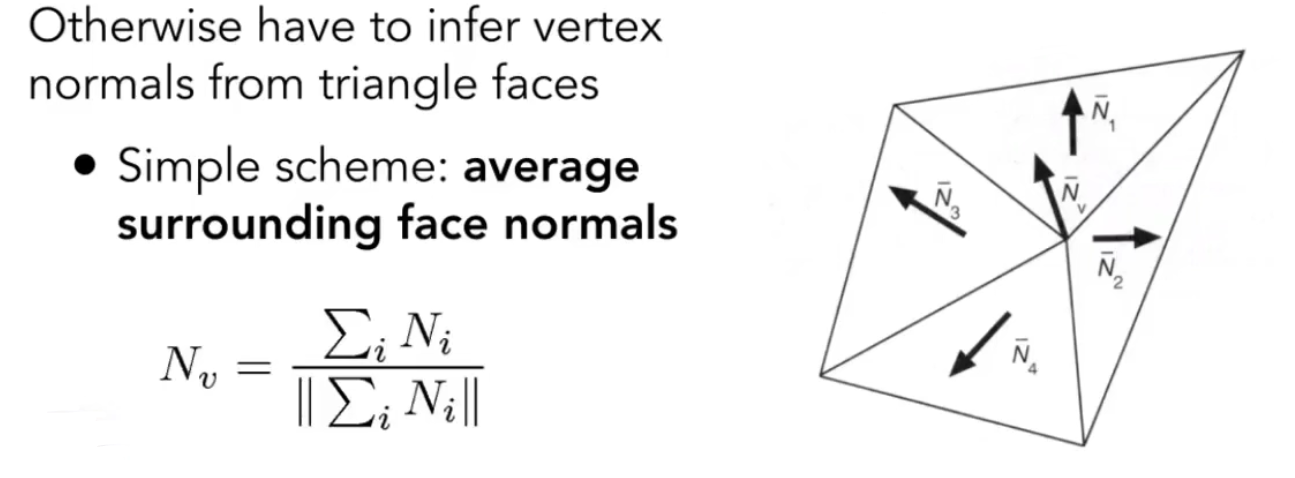
每个像素的法线通过插值顶点法线来获得

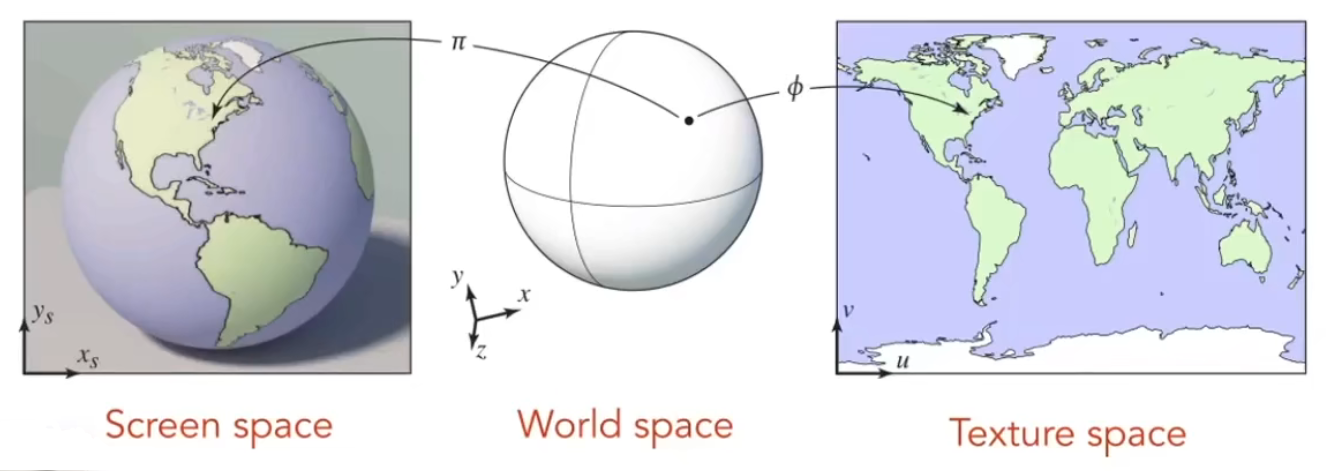
1.1.9 Texture纹理映射

任何一个三维物体都可以展开成一个二维的图，也就是可以用二维图片映射到三维物体上

Unity Shader

2.1基础知识

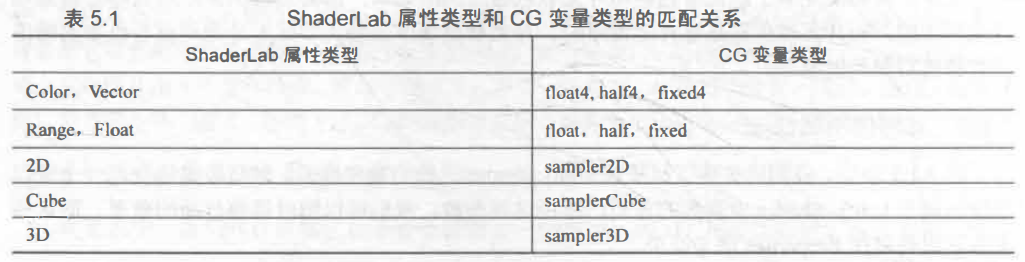
（Properties）ShaderLab属性类型和CG变量类型的匹配关系

（头文件）Unity中一些常用的包含文件

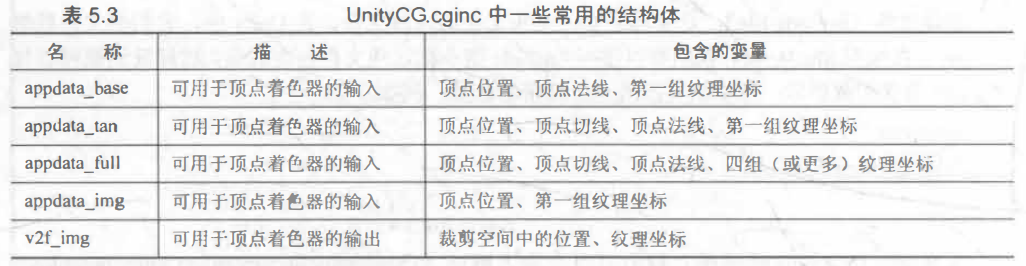
UnityCG.cginc中一些常用的结构体

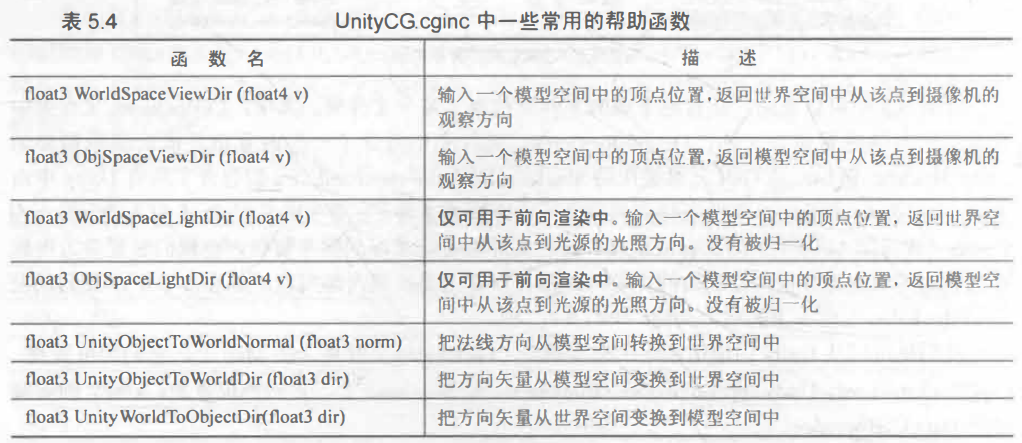
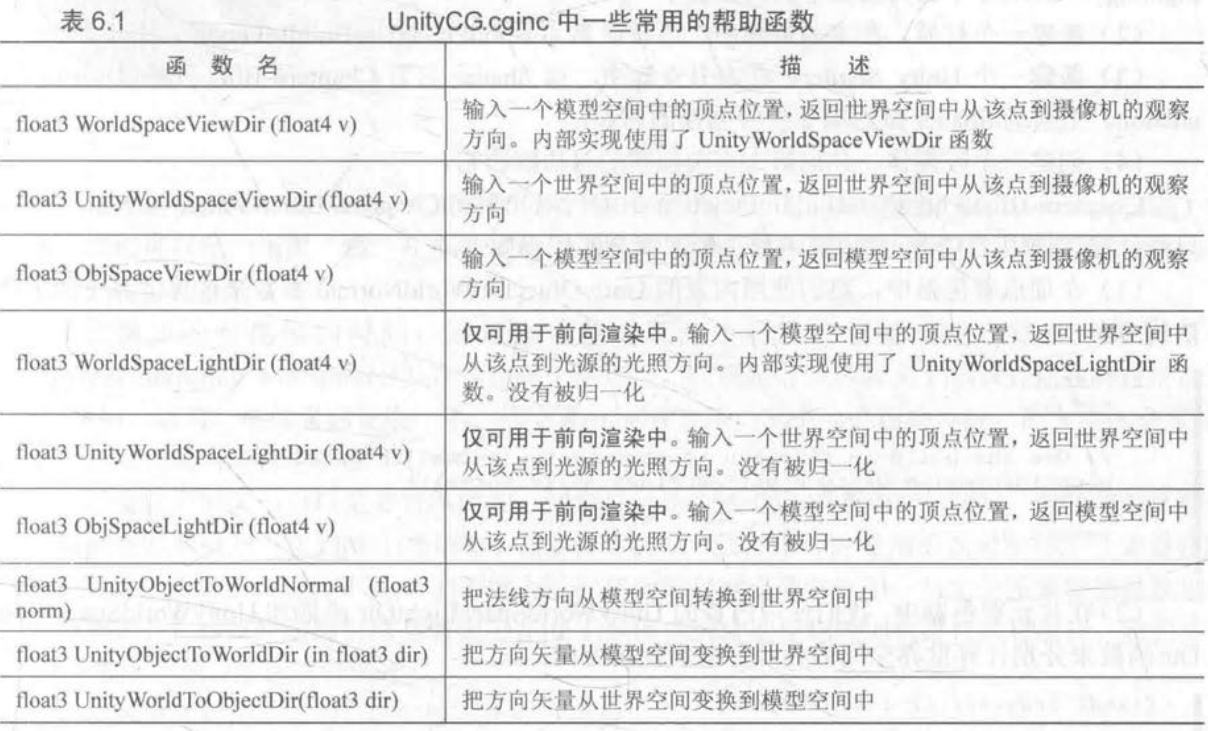
UnityCG.cginc中一些常用的帮助函数

从应用阶段传递模型数据给顶点着色器时Unity支持的常用语义

从顶点着色器传递数据给片元着色器时Unity使用的常用语义

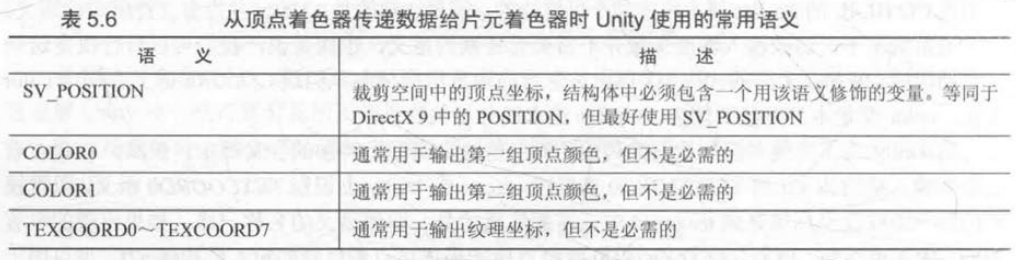
从片元着色器输出时Unity支持的常用语义

CG/HLSL中3中精度的数值类型

着色器编译目标级别 - Unity 手册 (unity3d.com) Unity支持的Shader Target

UnityCG.cginc中一些常用的帮助函数

2.1.1 Properties

开放在材质面板的参数

属性类型 默认值的定义语法 例子
Int number _Int(“整数”, Int) = 2
Float number _Float(“浮点数”, Float) = 1.5
Range(min, max) number _Range(“范围”, Range(0.0, 5.0) = 3.0
Color (n,n,n,n) _Color(“颜色”, Color) = (1, 1, 1, 1)
Vector (n,n,n,n) _Vector(“向量”, Vector) = (2, 3, 6, 1)
2D “defaulttexture” {} _Tex2D(“漫射图”, 2D) = “” {}
Cube “defaulttexture” {} _Cube(“Cube”, Cube) = “White” {}
3D “defaulttexture” {} _Tex3D(“3D”, 3D) = “black” {}

2.1.2 SubShader

  • [RenderSetup] 渲染状态的设定

常见的渲染设置选项

状态名称 设置指令 解释
Cull Cull Back | Front | Off 设置剔除模式，剔除背面/正面/关闭剔除
ZTest ZTest Less Greater | LEqual | GEqual | Equal NotEqual | Always 设置深度测试时使用的函数
ZWrite ZWrite On | Off 开启/关闭深度写入
Blend Blend SrcFactor DstFactor 开启并设置混合模式
  • [Tags] 渲染标签的设定

Tags是一个键值对（Key/Value Pair），键和值都是字符串类型，标签结构如下

1
2
3
4
5
Tags{ "TagName1" = "Value1" "TagName2" = "Value2" }
SubShader{
Pass{
//定义该Pass的光照模式为
Tags{ "LightMode" = "ForwardBase" }

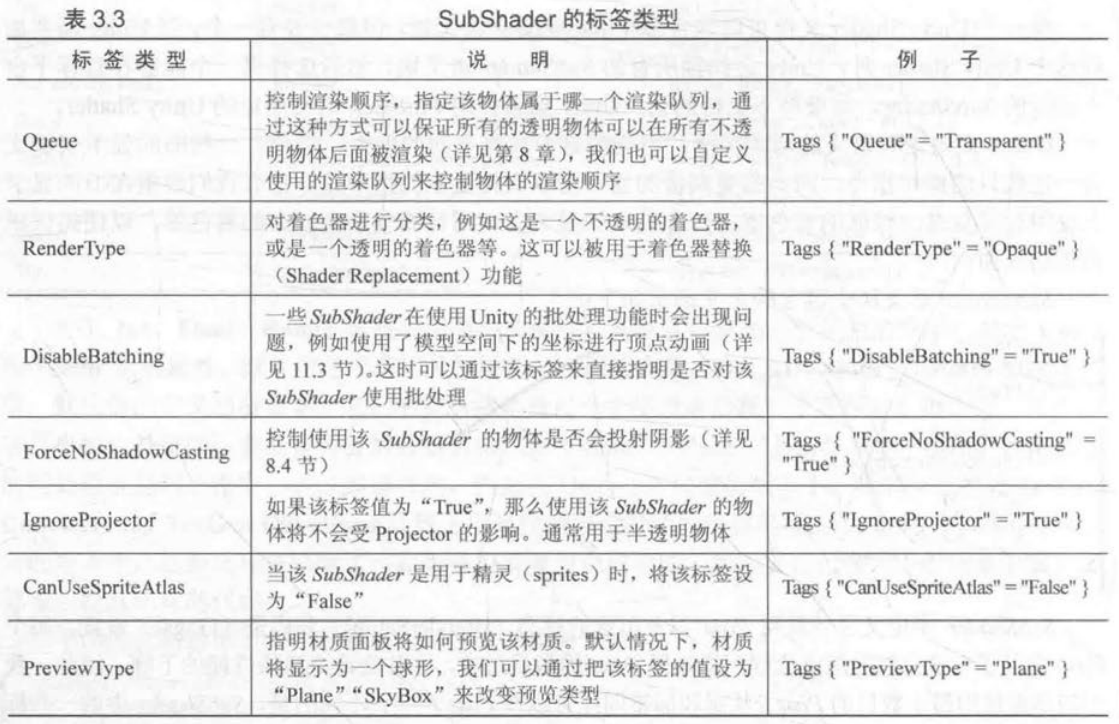
2.1.3点积和叉积

  • 点积dot计算公式一：对应分量相乘后相加

向量a点积单位向量b，得到的是a在单位向量b上的投影长度

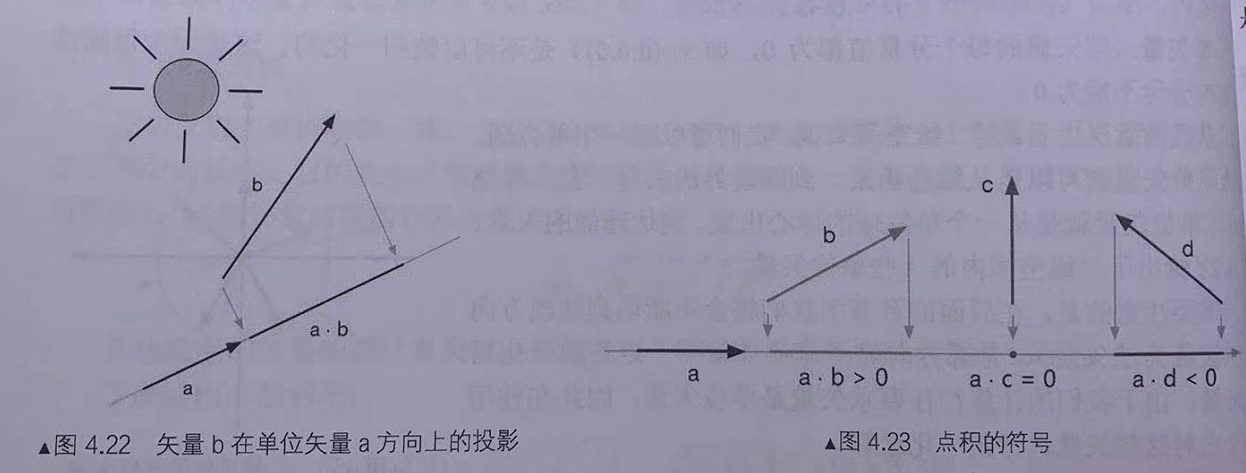
  • 点积计算公式二：模*模*cosθ

结果 > 0则表示两向量夹角<90°（同向），结果 < 0表示两向量夹角>90°（逆向）

  • 叉积corss计算公式 a×b = (ax,ay,az)×(bx,by,bz)=(aybz-azby,azbx-axbz,axby-aybx)

叉积不满足交换律和结合律a×b≠b×a，(a×b)×c≠a×(b×c)

实际上a×b=-(b×a)

|a×b|=|a||b|sinθ

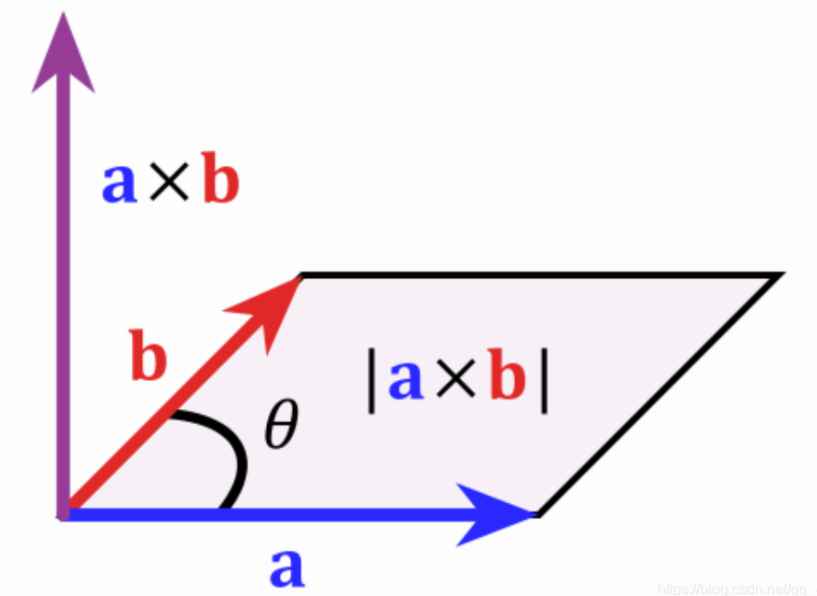
2.1.4矩阵

矩阵乘法：第i行*第j列就是第i j个元素，可以把第一个矩阵放在左侧，第二个矩阵放在上侧。

矩阵乘法不满足交换律。

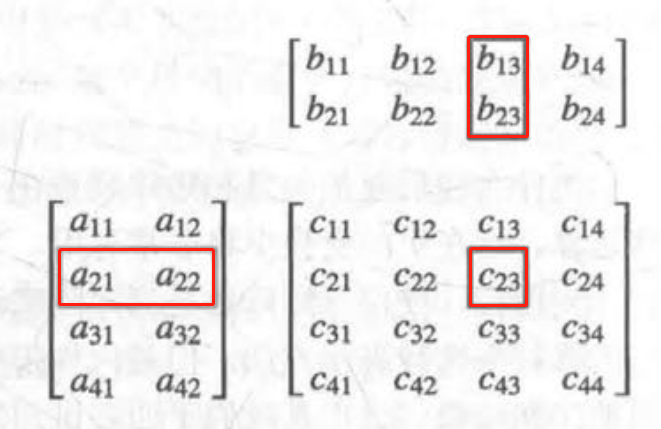
对角矩阵：除了m11、m22、m33都为0的矩阵

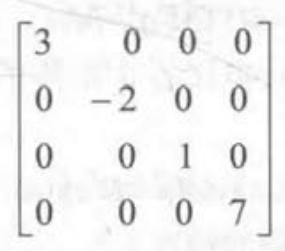
单位矩阵：对角矩阵的数值为1，用In来表示（MI=IM=M）

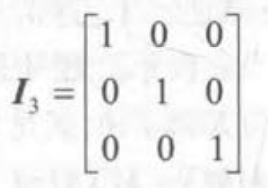
转置矩阵：将行列互换

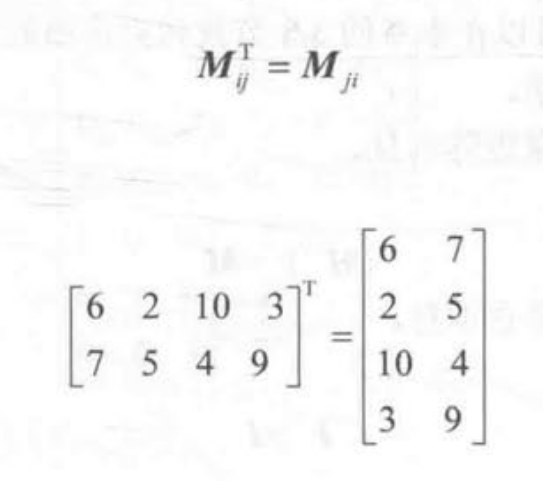
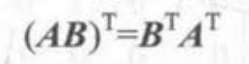
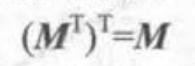
逆矩阵：只有方阵存在逆矩阵。如果一个矩阵的行列式不为0，则该矩阵存在可逆矩阵。

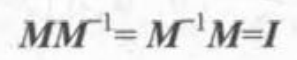
如果一个函数存在可逆矩阵，则存在如下性质。（例如可以对v矩阵经过M变换后再乘逆矩阵返回v）

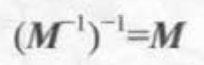
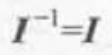
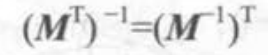
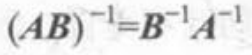
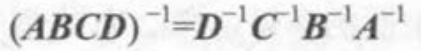
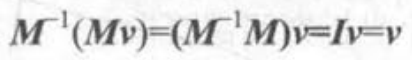
正交矩阵：特殊的方阵 如果方阵和它的转置方阵乘积为单位矩阵的话，称这个矩阵正交

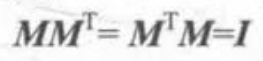
等价于

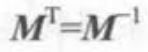
矢量（unity中为列矩阵）放在左侧和右侧乘以一个矩阵变换结果不同，unity中会放在矩阵右侧。

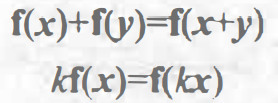
2.1.5矩阵的几何意义：变换

  • 线性变换：可以保留矢量加、标量乘的变换，用数学公式表示为
  • 齐次坐标：为了解决3×3的矩阵不能表示平移操作，所以将其扩充到4×4的矩阵

对于坐标，在齐次坐标中将w分量设置为1；对于矢量，将w坐标设置为0

平移矩阵：

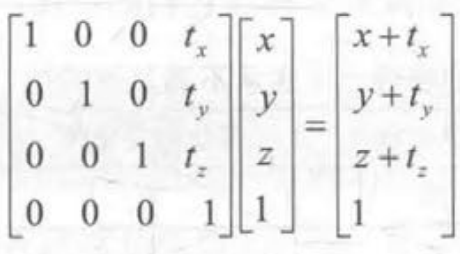
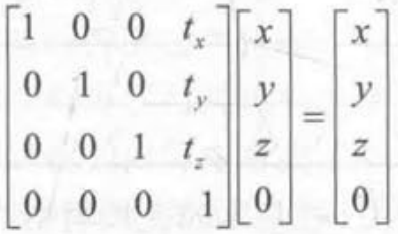
变换矩阵×坐标矩阵，得到坐标平移 平移矩阵×适量矩阵 矢量不变，平移不影响矢量

缩放矩阵：

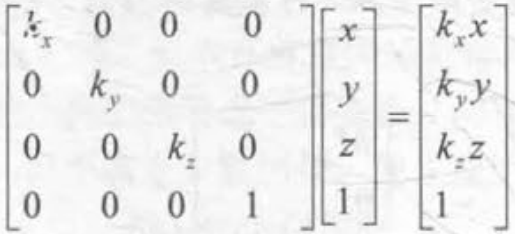
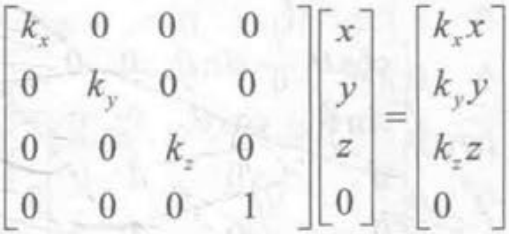
缩放对坐标和向量都起作用

复合变换：在绝大多数情况下，我们约定变换的顺序就是先缩放，再旋转，最后平移

2.1.6常用向量和所在空间表示

常用向量：

nDir： 法线方向 tDir： 切线方向 bDir： 副切线方向

lDir： 光照方向（的反方向） vDIr： 观察方向（的反方向） rDir： 光反射方向

hDIr： 半角方向

所在空间：

OS： ObjectSpace物体空间 WS： WorldSpace世界空间

VS： ViewSpace观察空间 CS： HomogenousClipSpace齐次剪切空间

TS： TangentSpace切线空间 TXS： TextureSpace纹理空间

举例：

nDirWS：世界空间下的法线方向

2.1.7单双面显示

1
2
3
4
5
6
7
    Properties{
        [Enum(UnityEngine.Rendering.CullMode)]_CullMode("CullMode", float) = 2
    }
      SubShader{
        Pass{
        Cull [_CullMode]
}}

2.2漫反射-Lambert

输入结构：

1
2
float4 vertex : POSITION;       //模型顶点信息
float3 normal : NORMAL;         //模型法线信息

输出结构：

1
2
float4 pos : SV_POSITION;       //屏幕空间顶点信息
float3 nDirWS : TEXCOORD0;      //世界空间法线信息

像素Shader：

1
2
3
4
VertexOutput o = (VertexOutput)0;                   //新建一个输出结构
o.pos = UnityObjectToClipPos(v.vertex);            //OS>>>CS
o.nDirWS = UnityObjectToWorldNormal(v.normal);    //OS>>>WS
return o;                                             //将输出结构输出

顶点Shader

1
2
float nDotl = dot(i.nDirWS,ldir);                   //nDir点积IDir
float lambert = max(0.0,nDot1);

2.3镜面反射-Specular-Phong

反射有明显的方向性，观察者视角决定了反射光线的有无。

Phong（r dot v）：即光反射方向和视角方向约重合，反射越强；

Blinn-Phone（n dot h）：即法线方向和半角方向越重合，反射越强；

power节点：类似于正片叠底，会让高光保存，其他地方变黑，取0到90。

2.4通过nDir表达顶底关系

nDir的RGB分别表示左右，顶底，前后三个方向。

通过Vector Operations里的Component Mask将nDir分解成RGB方向。

通过Color来表示环境光的颜色Occlusion

2.5 unity内置投影代码调用方法

1
2
3
4
5
6
#include "AutoLight.cginc"          //使用unity投影必须包含这两个库文件
#include "Lighting.cginc"           //使用unity投影必须包含这两个库文件
#pragma multi_compile_fwdbase_fullshadows
LIGHTING_COORDS(3,4)					//输出结构
TRANSFER_VERTEX_TO_FRAGMENT(o)		//顶点Shader	
float shadow = LIGHT_ATTENUATION(i);	//像素Shader

2.6 normal法线信息

normal：法线信息是切线空间的法线信息。

切线空间：切线空间由法线、切线和副切线共同构成，每个点都有一个切线空间。

顶点Shader：

1
2
3
4
5
o.nDirWS = UnityObjectToWorldNormal(v.normal);                   //OS>>>WS 
o.tDirWS = normalize(mul( unity_ObjectToWorld, 
                           float4(v.tangent.xyz, 0.0)).xzy);      //OS>>>WS
o.bDirWS = normalize(cross(o.nDirWS, o.tDirWS) * v.tangent.w); //OS>>>WS

像素Shader：

1
2
3
float3 nDirTS = UnpackNormal(tex2D(_NormalMap, i.uv0));     //切线空间的法线方向
float3x3 TBN = float3x3(i.tDirWS, i.bDirWS, i.nDirWS);      //TBN矩阵
float3 nDirWS = normalize(mul(nDirTS, TBN));                //转换为世界空间方向

此时的nDirWS就是通过法线贴图定义的模型法线方向了

2.7 Fresnel菲尼尔效果

通过vDotn获取视角向量和法向量的点积值

使用1-vDotn就可以获得Fresnel效果，再使用Pow控制强度即可。

2.8 Matcap模拟环境效果（TBN矩阵 / 法线向量）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//TBN矩阵（切线空间法线贴图转换为世界空间法向量）（Matcap）
//输入结构
float3 normal : NORMAL;
float4 tangent : TANGENT;
//输出结构
float3 nDirWS : TEXCOORD1;      //n WS
float3 tDirWS : TEXCOORD2;      //t WS
float3 bDirWS : TEXCOORD3;      //b WS
//顶点Shader
o.nDirWS = UnityObjectToWorldNormal(v.normal);
o.tDirWS = normalize(mul( unity_ObjectToWorld, float4(v.tangent.xyz, 0.0)).xzy);
o.bDirWS = normalize(cross(o.nDirWS, o.tDirWS) * v.tangent.w);
//像素Shader
float3 nDirTS = UnpackNormal(tex2D(_NormalMap, i.uv0));
float3x3 TBN = float3x3(i.tDirWS, i.bDirWS, i.nDirWS);
float3 nDirWS = normalize(mul(nDirTS, TBN));
float3 nDirVS = mul(UNITY_MATRIX_V, float4(nDirWS, 0.0));
float2 matcapUV = nDirVS.rg * 0.5 + 0.5;
float3 matcap = tex2D(_Matcap,matcapUV);

Shader进阶

模型外扩溶解动画（02_Tube）

设置好模型UV后，通过黑白贴图和黑白噪波贴图采样模型UV，获取其中r/g/b某一个值，然后通过clip函数进行裁剪，就可以获得溶解的效果

1
2
3
4
5
6
7
float4 frag( vertexOutput i) :SV_Target{
       float flow = tex2D(_FlowTex, i.uv0 + _Time.y * _FlowSpeed.xy).r;
       float noise = tex2D(_NoiseTex, i.uv0 + _Time.y * _FlowSpeed.zw).r;
       clip(flow - _Cutoff - noise);
       float flowAplha = flow * _DiffuseCor.a;
       return _DiffuseCor;
}

半透明模型扫光动画（03_Scan）

半透明物体所需标签和Pass（该ZWrite方法会完全消除透明物体内部可见的轮廓）见附录2

半透明效果：利用菲尼尔原理计算出的(0,1)值来控制透明通道，可以得到菲尼尔的透明效果。

扫光效果：通过世界坐标的xy作为uv值，将扫光的贴图以该uv进行计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
float3 vDirWS = normalize(_WorldSpaceCameraPos - i.posWS);
float3 nDirWS = i.nDirWS;
//flow uv采样 这里使用世界坐标的xy作为uv，可以让整个动画看起来像从上到下播放。获取轴点的世界坐标，与模型世界坐标相减，可以得到一个固定差值
float2 piovtWS = mul(unity_ObjectToWorld,float4(0.0,0.0,0.0,1.0));
float2 posWS = i.posWS.xy;
float2 uv1 = (posWS - piovtWS) * _FlowTex_ST.xy + _FlowTex_ST.zw;
float flowUValpha = max(0,tex2D(_FlowTex, uv1 + _Time.y * _Speed).r - 0.7);
//贴图增加Fresnel细节
float fresnelTexAlpha = tex2D(_FresnelTex, i.uv0).x;
//Fresnel控制中间不透明边缘透明
float vdotn = max(0,dot(vDirWS,nDirWS));
float fresnelAlpha = min(mul(pow(1 - vdotn, _FresnelPow),_FresnelInt) + _FresnelAll,1);
float4 fresnelColor = lerp(_InnerColor,_MipColor,fresnelAlpha);
float finallAlpha = min(1,fresnelAlpha+flowUValpha+fresnelTexAlpha);
return float4(fresnelColor.xyz,finallAlpha);

生长动画（05_Grow）

控制模型生长：通过clip函数和uv值(0,1)来控制像素Shader显示的范围。

控制模型整体缩放：在顶点Shader中，通过控制顶点 ± 法线 * 数值来控制顶点的偏移量。

控制模型部分缩放：通过模型uv值(0,1)和smoothstep函数可以获取一段范围，再将模型缩放与这段范围 相乘就可以控制该部分的缩放。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
vertexOutput vert (vertexInput v)
{
    vertexOutput o;
    //模型整体缩放控制
    float4 vertexZhengti =float4(v.normal.xyz * _Expand,0);
    //模型尖尖缩放控制，控制缩放的范围
    float jianQuyu = smoothstep(_Cutoffmin,_Cutoffmax,(v.uv0.y - _Cutoff));
    float4 vertexJian =float4(v.normal.xyz * _Expand2,0) * jianQuyu;
    //模型顶点移动和
    float4 newVertex = v.vertex + vertexZhengti - vertexJian;
    o.vertex = UnityObjectToClipPos(newVertex);
    o.uv0 = v.uv0;
    return o;
}
float4 frag (vertexOutput i) : SV_Target
{
    //通过像素Shader进行模型裁切
    clip(_Cutoff - i.uv0.y);
    return 1;
}

魔镜效果（06_Mirror）

魔镜区域：Queue为2460，将“魔镜”的ColorMask设置为0，表示不渲染颜色。

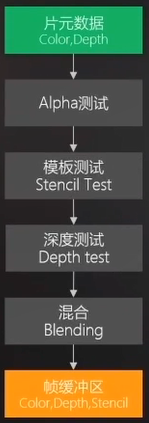
设置它的模板缓冲区参考值为1（默认为0）；通过模板缓冲测试规则的比较方式为always；通过后模板缓冲测试的值默认为不变，这里设置为replace替换，此时模板缓冲区该魔镜的范围都为1。

我们不需要写入深度，否则会遮挡后面的物体，所以ZWrite off。

1
2
3
4
5
6
7
8
9
10
        Tags { "Queue"="AlphaTest+10" }
        Pass{
            ColorMask 0
            Stencil{
                Ref 1
                Comp always
                Pass replace
            }
            ZWrite off
        }

魔镜内物体：Queue为2470，设置模板缓冲参考值为1，只有该部分数值等于1时，才会显示。

1
2
3
4
5
6
        Tags { "Queue"="AlphaTest+20" }
        Pass{
            Stencil{
                Ref 1
                Comp equal
            }

遮挡边缘物体：此时从魔镜内还可以看到其他已经渲染（Queue2000）的物体，创建一个球体，放大几百倍。设置它的Queue为2465，比魔镜内物体提前渲染，将深度测试设置为Always永远可以通过。此时他将首先在魔镜内遮挡其他所有物体，因为无限远，所以后面再生成的魔镜内物体可以正常显示。

1
2
3
4
5
6
7
8
        Tags { "Queue"="AlphaTest+15" }
        Pass{
            Stencil{
                Ref 1
                Comp equal
            }
            Ztest Always
            Cull front

火焰效果（Step / SmoothStep）（10）

1
2
3
4
//x和A进行比较，x较大则返回1，否则返回0
Step(A,x);
//x和A、B进行比较，x大于B则返回1，x小于A则返回0，x介于A和B之间进行插值计算
SmoothStep(A,B,x);

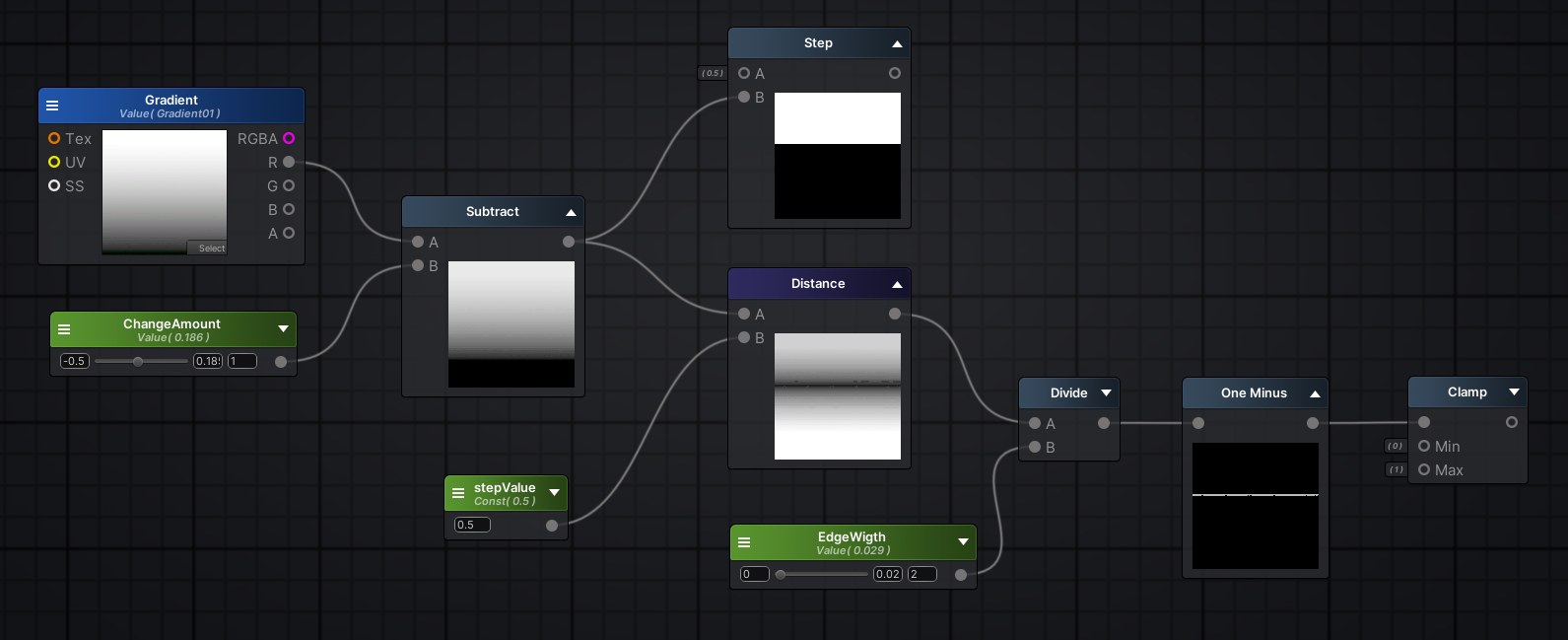
边缘燃烧消失效果（Distence）（11）

1
2
3
4
5
//返回A到B的距离
Distence(A,B);
//通过Step函数限制小于0.5的为0，大于0.5的为1
//将数值输出到clip就可以获得像素裁剪的效果
//通过Distence函数获取该点到0.5的距离就可以获得一个限制边缘的效果

附录

常用向量

1
2
3
4
5
6
//常用向量
float3 posCS = UnityObjectToClipPos(v.vertex);
float3 posWS = mul(unity_ObjectToWorld, v.vertex);
float3 nDirWS = UnityObjectToWorldNormal( v.normal );
float3 vDirWS = normalize(_WorldSpaceCameraPos.xyz - i.posWS.xyz);
float distance = distanceAtoB(pointofOrign.xyz, posWS.xyz);

透明物体所需标签和Pass

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
        Tags { 
            "RenderType"="TransparentCutout"
            "Queue" = "Transparent"
            "IgnoreProjector" = "True" 
        }
        Pass{
            ZWrite On
            ColorMask 0
        }
        Pass{
            ZWrite Off
            //Scr是source color源颜色，Dst是destination color目标颜色
            //源颜色是片元Shader产生的颜色，目标颜色是颜色缓冲区读取的颜色
            //Scr * Aplha + Dst * (1-Alpha)
            Blend SrcAlpha OneMinusSrcAlpha
            //Scr * Alpha + Dst * 1 这种模式无论物体透明度如何都会结合Dst颜色，更柔和
            Blend SrcAlpha One

Author: mxwu

Permalink: https://mingxuanwu.com/2022/03/05/202203050620/

License: Copyright (c) 2023 CC-BY-NC-4.0 LICENSE

Tag(s): # unity
back · home