1. Transformation(转换)
线性变换:一个坐标,可以通过一个矩阵乘法获得到新的坐标
1.1 2D Rotate
我们知道这个图形上每一个点都满足这个矩阵变换,所以旋转矩阵可以通过某两个个特殊点带入计算获得。下图为一个点的例子。
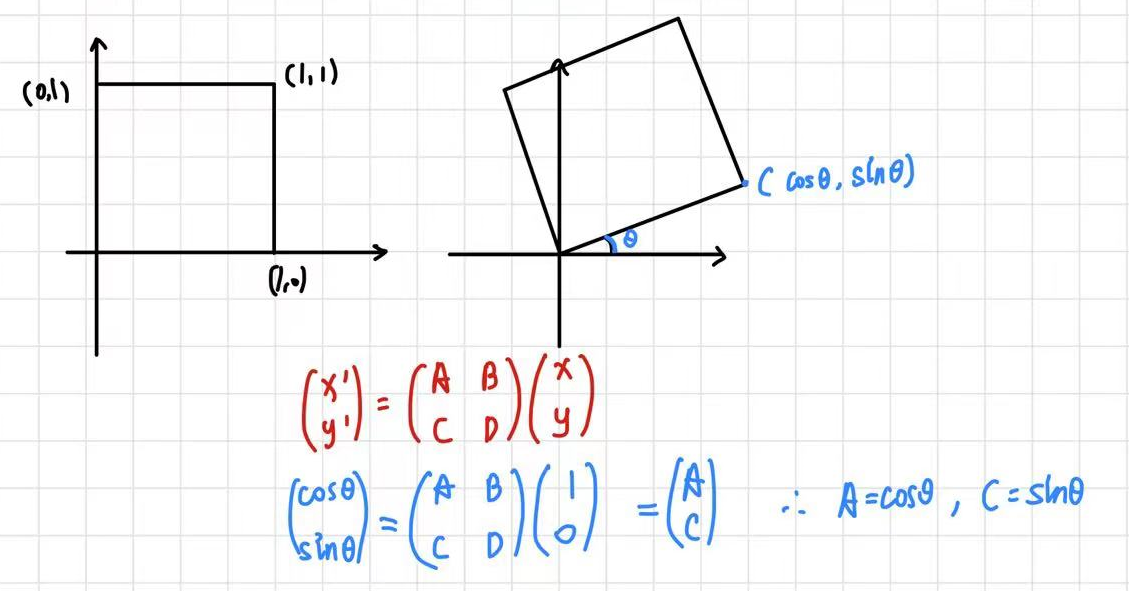
如果要旋转-θ角,把-θ带入①式可以得到,此时R-θ恰好是Rθ的转置,而且旋转θ角和旋转-θ角本身是一个互逆的操作。如果一个矩阵的逆恰好等于这个矩阵的转置,则称这种矩阵为正交矩阵。
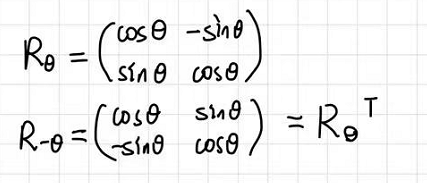
1.2 2D Translate
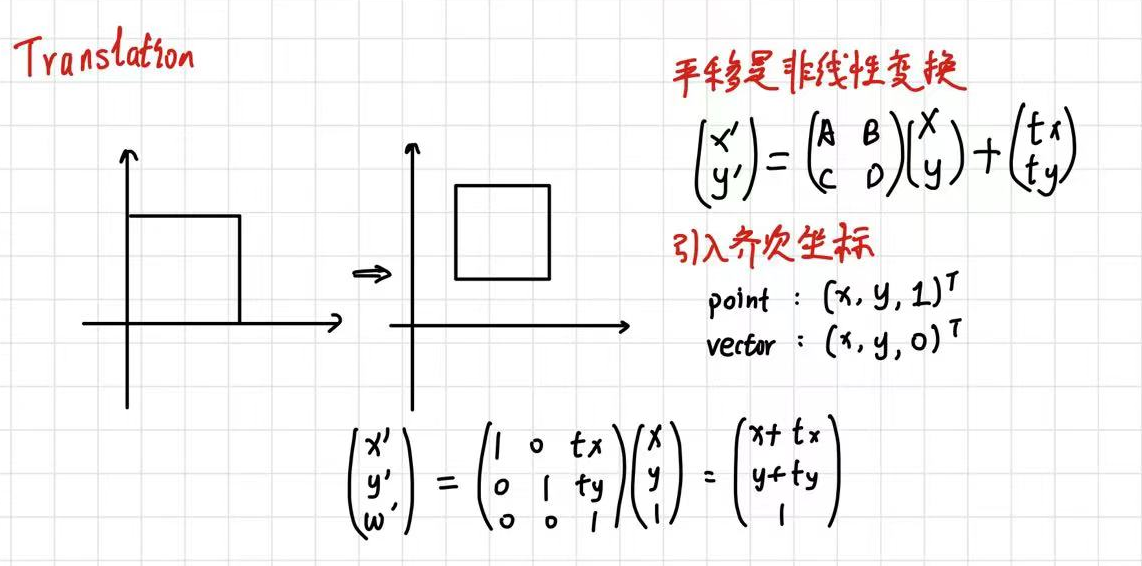
平移不满足线性变换,为了方便计算引入了齐次坐标。向量后加一个0,坐标后增加一个1,向量有平移不变性,而坐标平移后会变更。
而且根据下图还可以看出,齐次坐标相减会变为向量,向量相加还是向量,恰好正确
 |
 |
1.3 2D Composite Transformations
Order:Scale → Rotation → Translation,这里规定矩阵是从右向左乘的。
(顺序必须是上述顺序,例如沿y轴缩放,如果先旋转45°再缩放,会导致他发生形变)
 |
 |
如果想要旋转一个非原点的图形,需要先将他平移回原点,然后进行旋转,之后再平移回之前的位置。
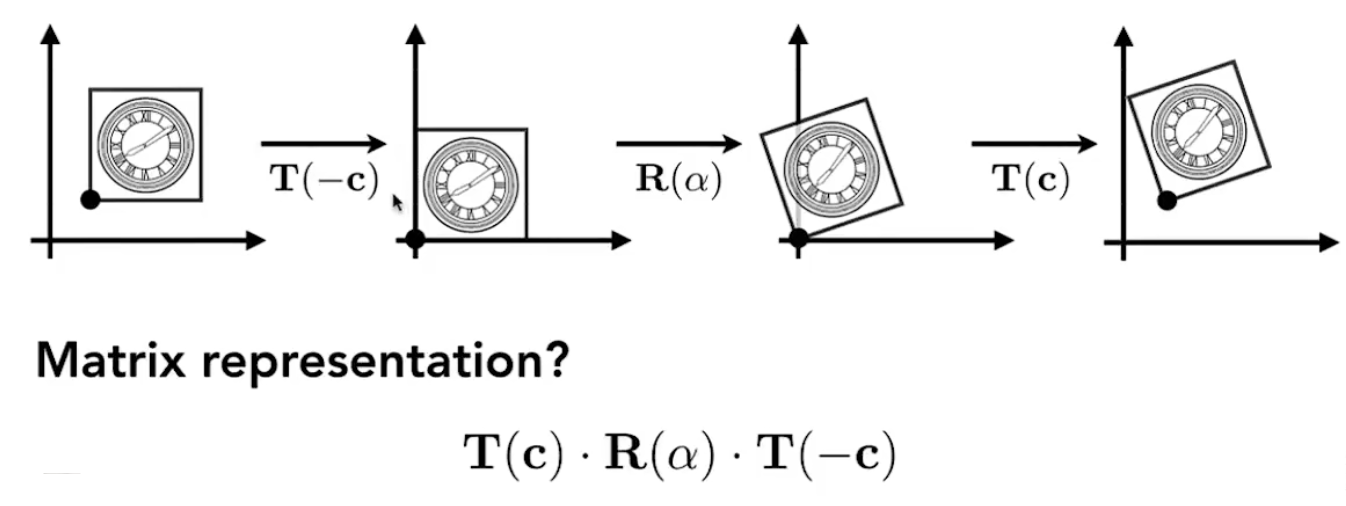
1.4 3D Transformations
这里x和z都是与2D相同的,y不同与叉乘方向有关。
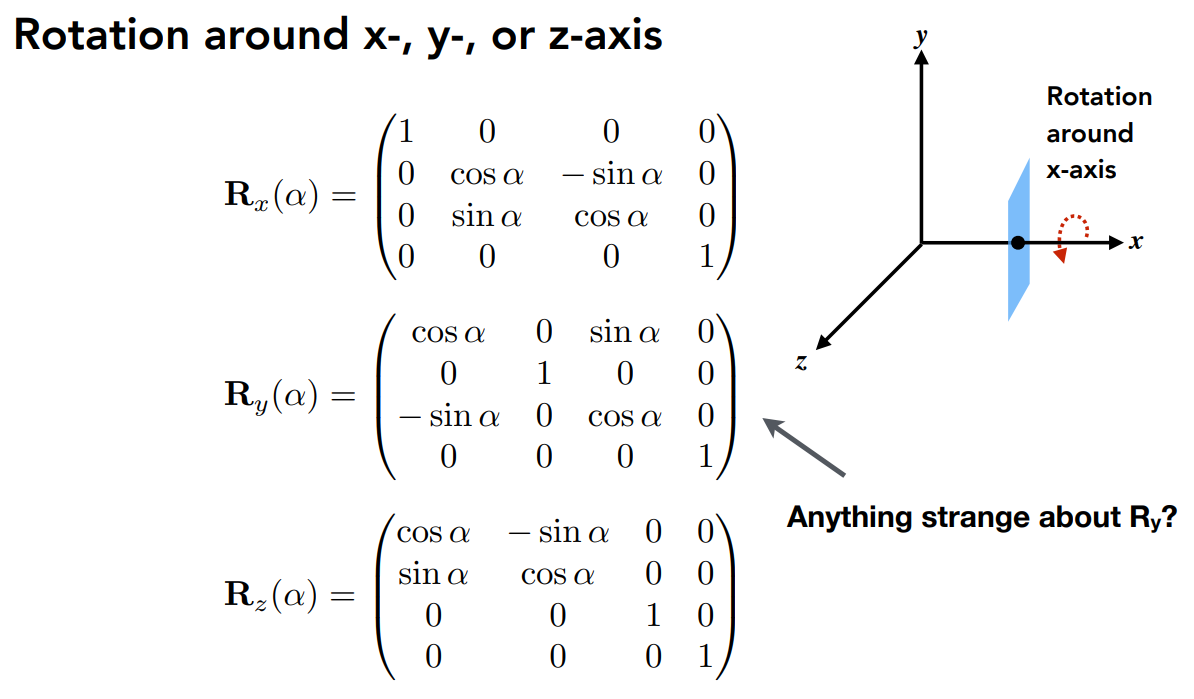
3D Rotations:组合RxRyRz三个轴的旋转
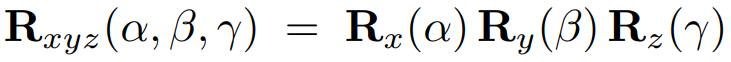

1.5 View/Camera Transformation
将摄像机转换到原点

2. Rasterization(光栅化)
2.1 Triangles(三角形)
for(int x = 0; x < xmax ; x++)
for(int y = 0; y < ymax ; y++)
inside(try, x+0.5, y+0.5) //是inside自己定义的函数,判断像素是否在连线内
如果像素在三角形内,则P0P2 × P0Q、P2P1 × P2Q、P1P0×P1Q 叉乘结果应该符号相同
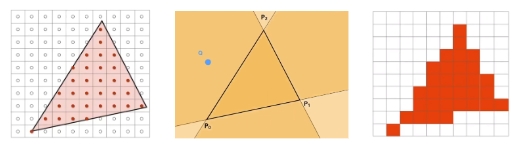
2.2 Antialiasing(抗锯齿)
由于光栅化的过程会出现走样的情况,锯齿很明显,提出了模糊的方法来解决锯齿问题,先进行模糊,再进行采样。

2.3 Fourier Transform(傅里叶变换)
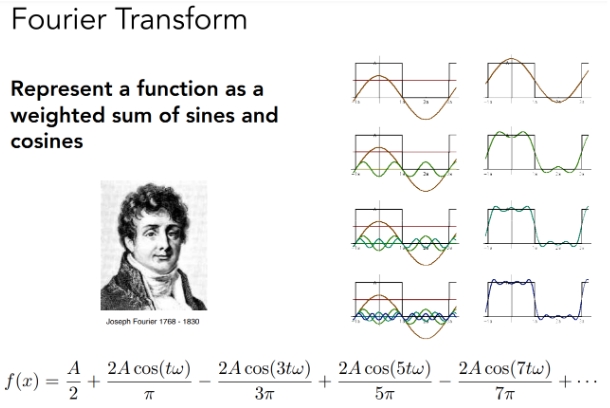
任何一个函数都可以分解成sin和cos组成的函数,也就是分解成了不同的频率(周期)函数的和。
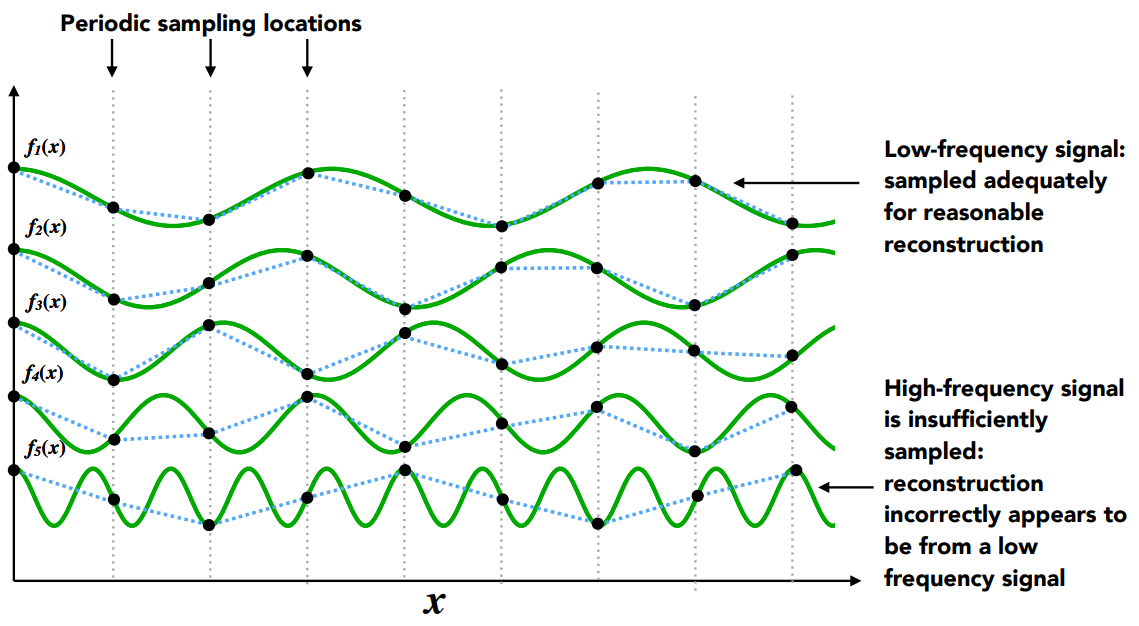
如果一个函数频率很高,必须用很高的采样频率才能正确的恢复出这个函数。
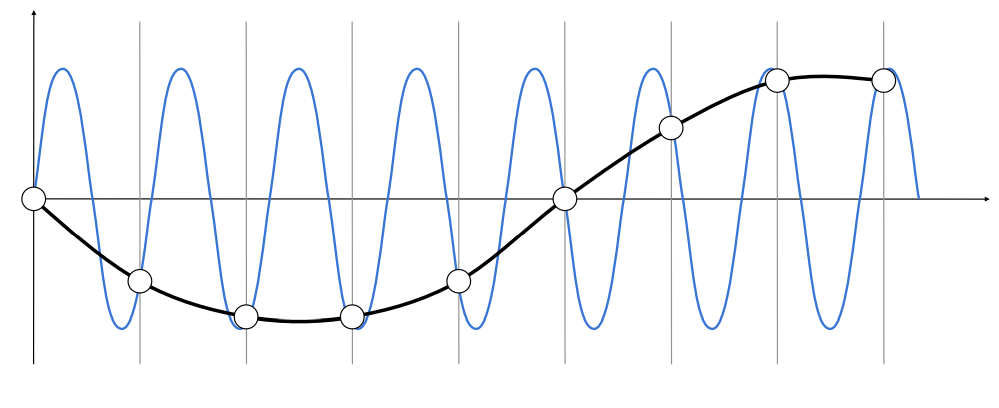
同样的采样方法,采样两个完全不同的函数,但得到的结果是完全相同的,就会产生走样。
2.4 Filtering(滤波)
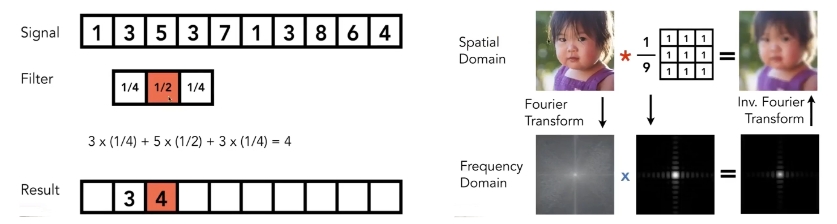
通过傅里叶变换将图片转换为频率(中心为低频信息,边缘为高频信息)

高通滤波,只显示高通信息,即对比度信息较高的信息;低通滤波与之相反,保留对比度较低的信息

2.5 Convolution(卷积)
可以理解为对该像素的信号做一个加权的平均值,取附近的信号和该像素的信号。比如右图3×3
MSAA,把1个像素当成4个像素进行处理来抗锯齿。还有FXAA、TAA、DLSS方法抗锯齿

2.6 Z-Buffer(深度缓冲)
//注,图形学中摄像机z轴正方向为从屏幕指向屏幕外,这里为了方便理解,将z轴指向屏幕内,所以数字越大深度越深
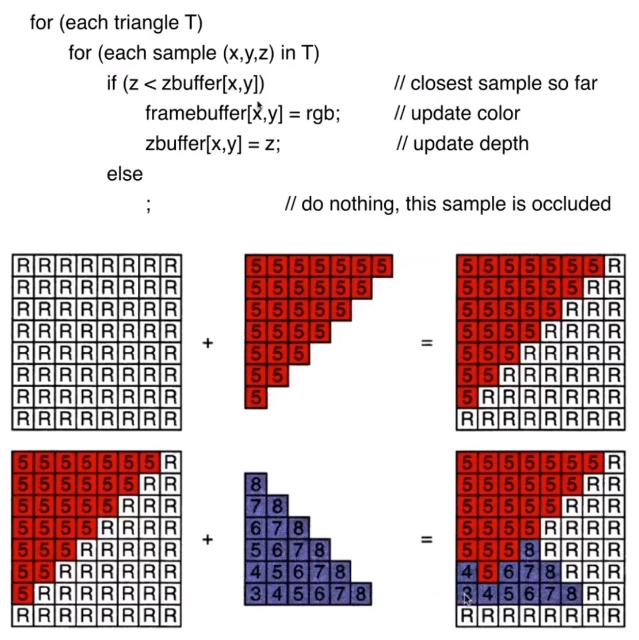
3. Shader(着色器)
3.1 Lambert Diffuse Shading
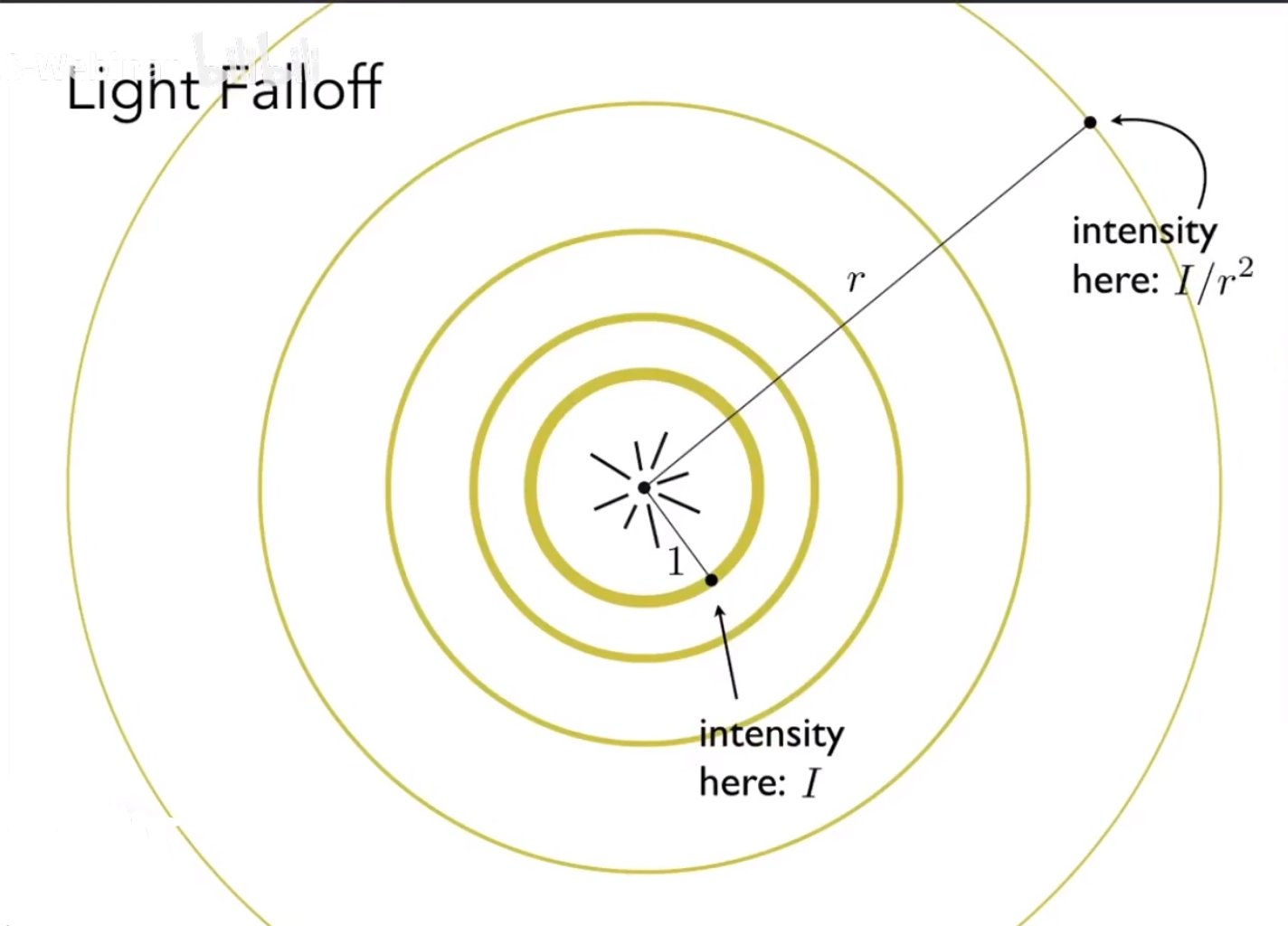
我们认为光的能量,在每一个球壳上是完全相等的,也就是说光的能量与半径的平方成反比
能量 = I/r2
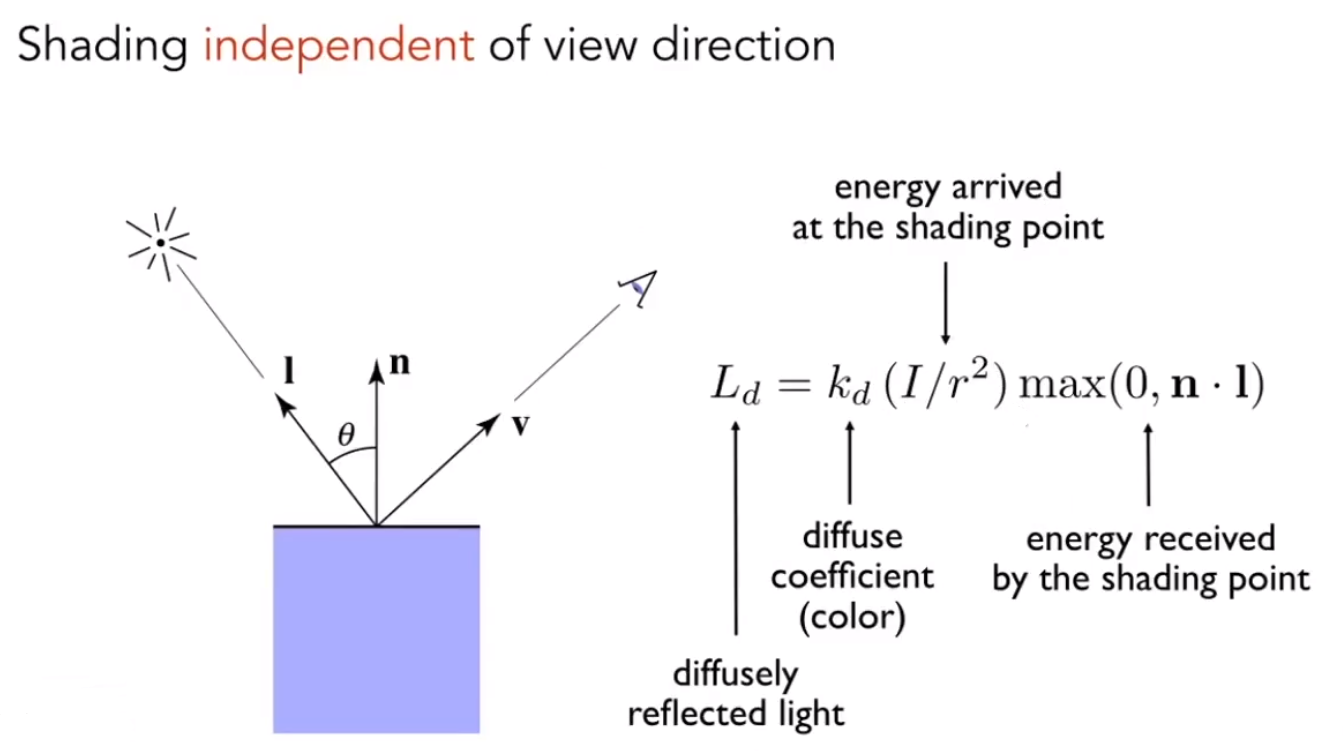
我们获得了光的能量计算方法,所以可以获得光能量影响下的兰伯特公式
hd = Kd(I/r2) max(0,n·l)

3.2 Blinn-Phong
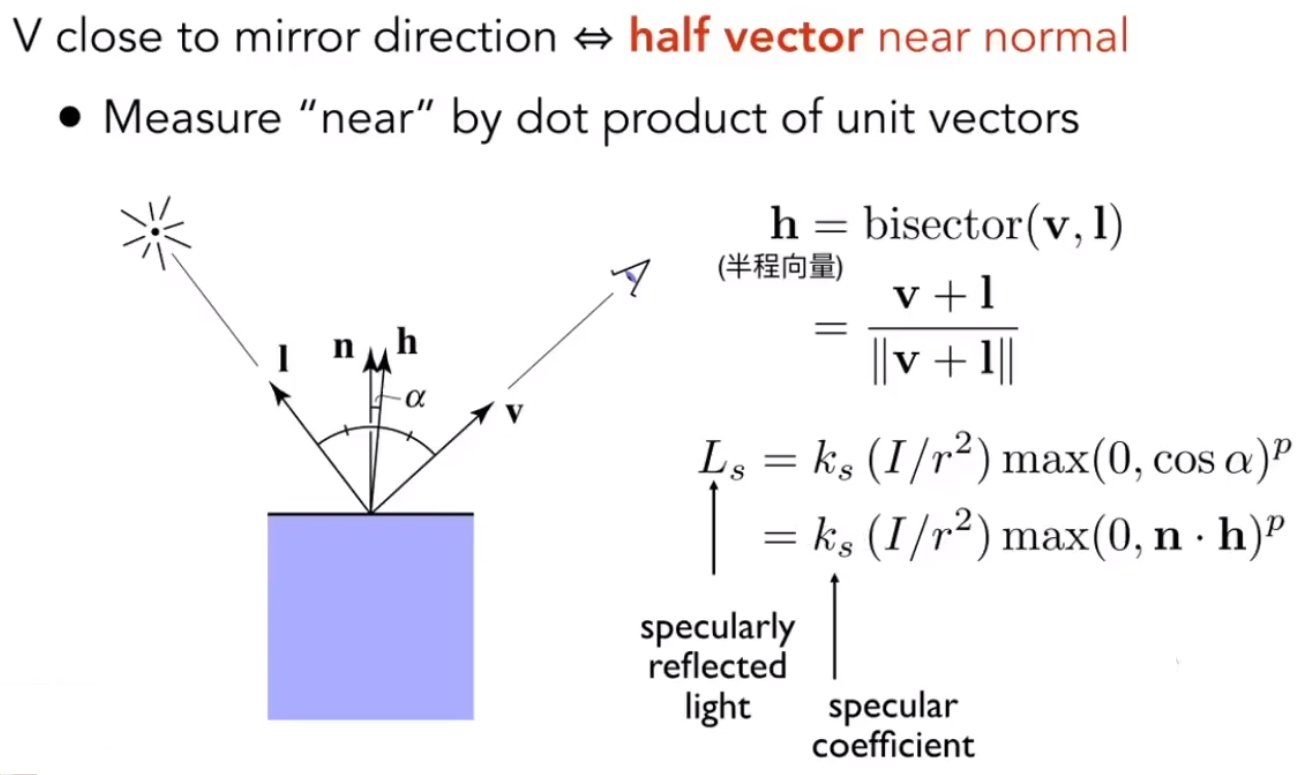
高光处p的指数主要用于缩小高光的范围,高光应该是人眼观测角度很小时才有的现象,下图为高光次幂
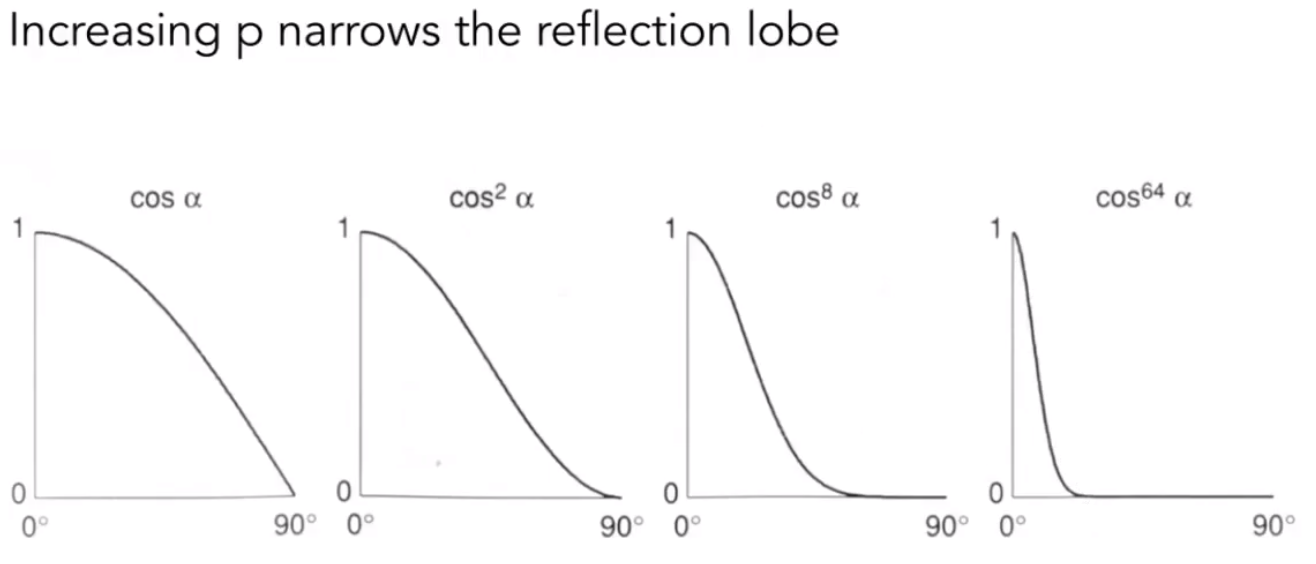
3.3 Ambient
环境光可以理解为是一个均匀的光,整体完全提亮
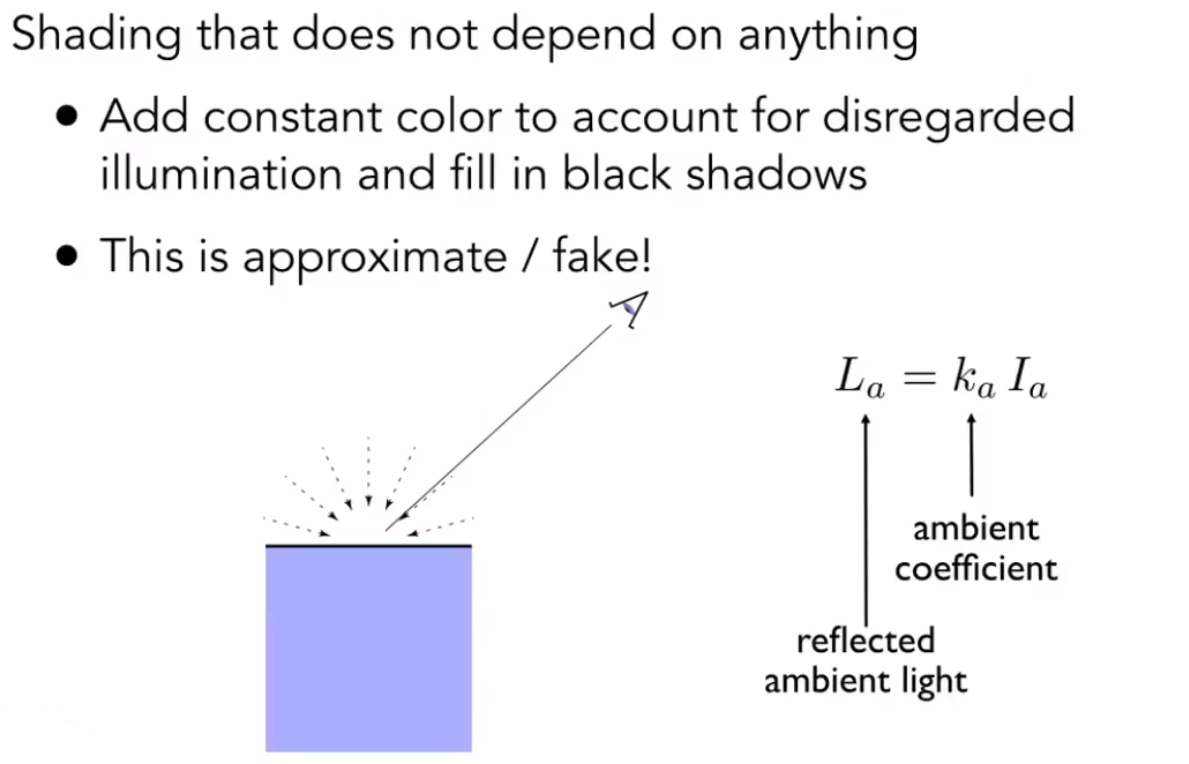
3.4 Blnn-Phong Reflection Model

3.5 Shading Frequencies
三种渲染模式:每个面的法线、每个顶点的法线、每个像素的法线

每个顶点法线的计算就是通过每个面的法线,经过加权平均以后获得顶点的法线
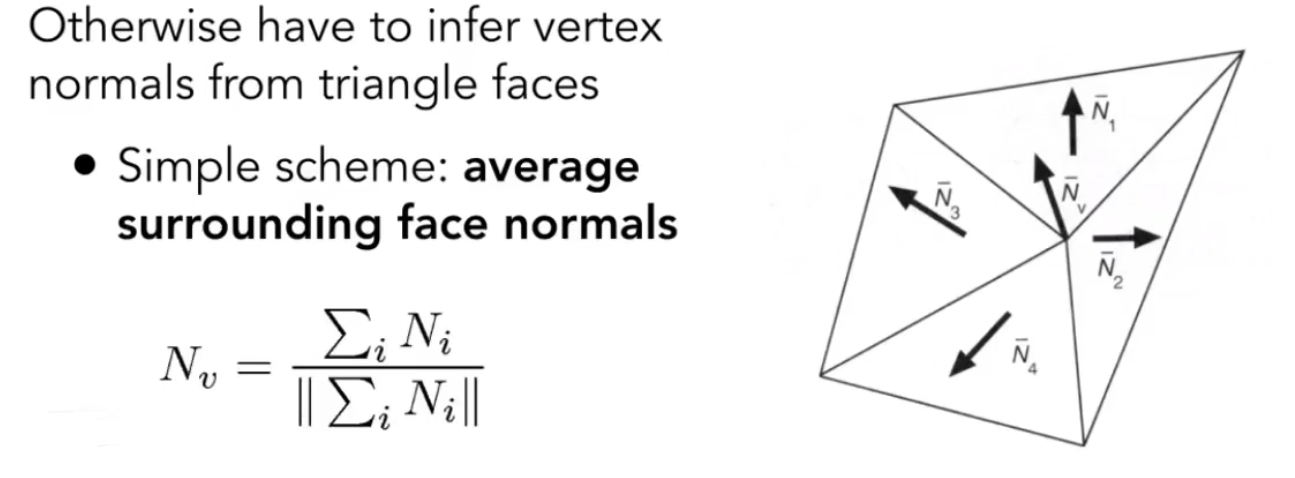
每个像素的法线通过插值顶点法线来获得
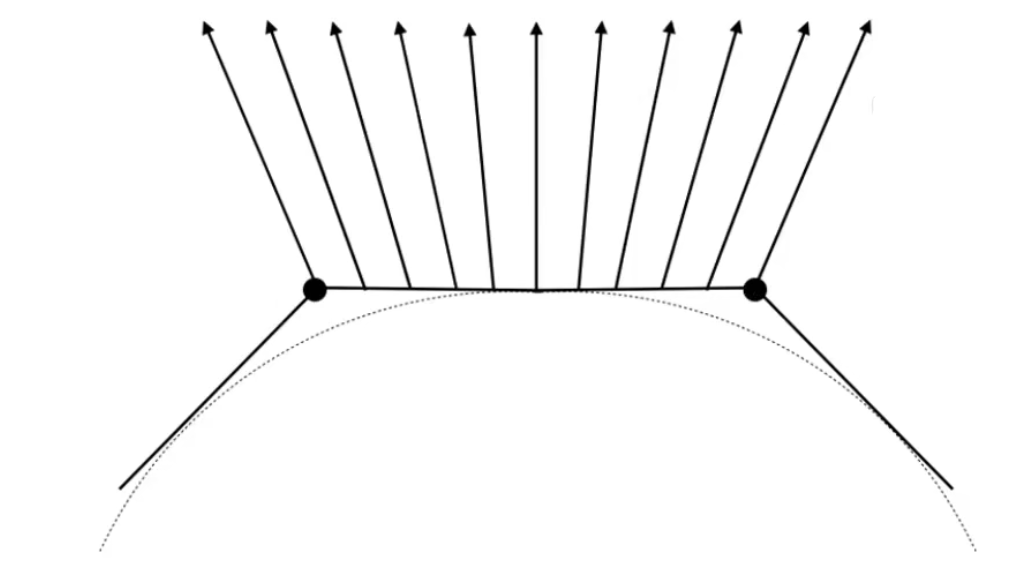
3.6 Texture mapping
任何一个三维物体都可以展开成一个二维的图,也就是可以用二维图片映射到三维物体上(0,1)之间

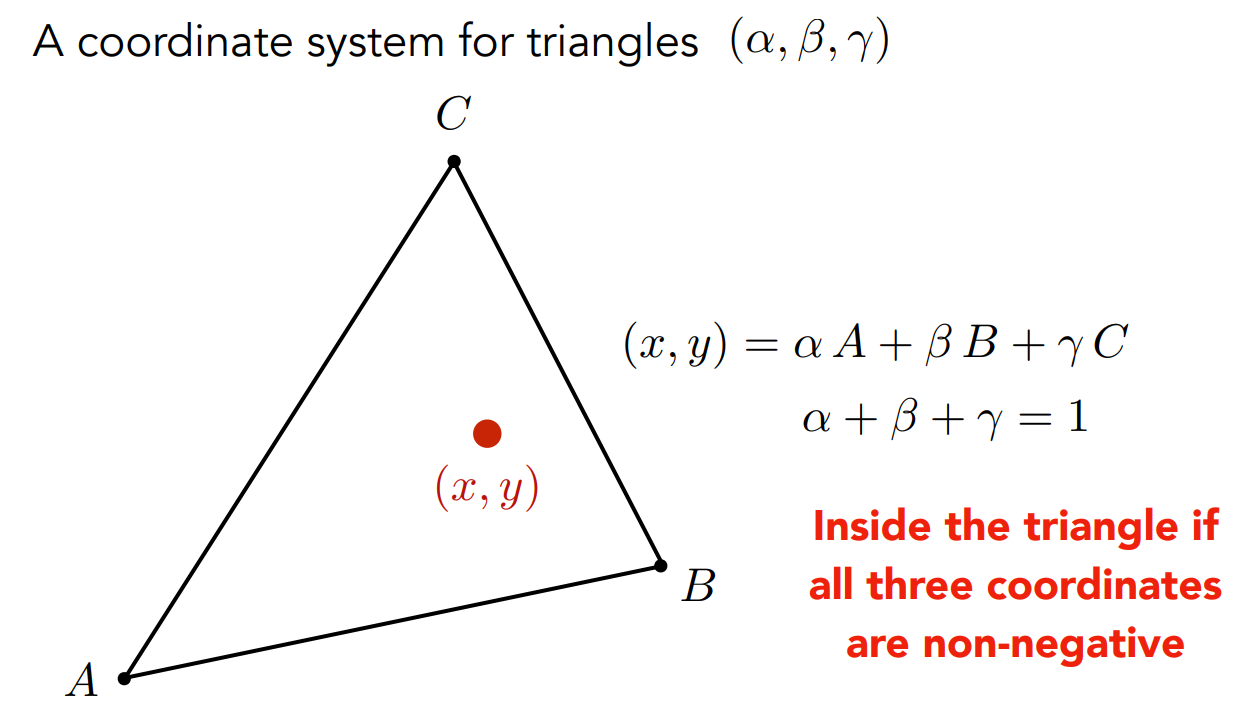
3.7 Barycentric Coordinates(重心坐标)
三角形所在平面内任意一点都可以表示为三角形三个顶点的线性组合,记为(****α,β,γ)
三角形ABC所在平面上任意一点**(x,y),且α+β+γ=1,都可以用(x,y)=αA+βB+γC**来表示,
如果满足**(α≥0,β≥0,γ≥0),则(x,y)**一定在三角形内。
这种表示的好处是,只要有3个点,不论在什么坐标系里,都可以用αβγ来表示坐标。
举例:A点的重心坐标是(1,0,0),B点的重心坐标为(0,1,0),C点的重心坐标(0,0,1)